review
딥러닝 기초
index

https://dbrang.tistory.com/1537
퍼셉트론
신경망
신경망 학습
오차역전파법
학습 관련 기술들
1.
퍼셉트론

퍼셉트론이란?

퍼셉트론 perceptron은 프랑크 로젠블라크가 1957년에 제안한 초기 형태의 인공신경망이다.
이 알고리즘은 신경 세포 뉴런의 동작을 모방하였다.
즉, 신경세포 뉴런이 가지돌기에서 '신호'를 받아, 이 신호의 크기가 '임계값'을 넘으면 축삭돌기를 통해 신호를 내보내는 것처럼,
다수의 신호를 받아 가중치를 부여한 뒤에 신호의 합이 임계치보다 크면 하나의 신호를 출력한다.
위 사진에서 x1, x2는 입력값, w1, w2는 가중치, y는 출력값에 해당한다.
가중치가 축삭돌기의 역할을 한다.
가중치가 클수록 입력값이 중요하다는 것을 의미한다.
입력값에 가중치가 곱해져 w1x1+w2x2가 되고,
이 값이 임계치(theta)보다 크면, 인공뉴런은 0을, 그렇지 않으면 1을 출력한다.
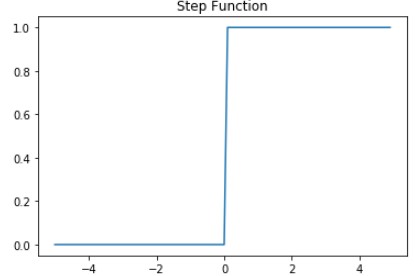
이러한 함수를 계단 함수 step function 이라고 한다.
단순한 논리회로
입력값 x1, x2를 이용해서 가장 간단한 논리 회로를 구성해볼 수 있다.
AND
| x1 | x2 | y |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
def AND_gate(x1, x2):
w1=0.5
w2=0.5
b=-0.7
result = x1*w1 + x2*w2 + b
if result <= 0:
return 0
else:
return 1
OR
| x1 | x2 | y |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
def OR_gate(x1, x2):
w1=0.6
w2=0.6
b=-0.5
result = x1*w1 + x2*w2 + b
if result <= 0:
return 0
else:
return 1
위의 예시는 w1=1, w2=1을 가정하였으나
가중치를 적절히 조정하면 다양한 퍼셉트론을 표현할 수 있다.
그리고 '학습'은 매개변수 값을 정하는 작업이라고 할 수 있다.
퍼셉트론의 한계
XOR 게이트
* XOR이란,
exclusive or라는 뜻으로
p, q 둘 중 하나일 때만 true인 논리 연산자이다.
https://tomatolife.tistory.com/114?category=1025465
[이산수학] 배타적 논리합 XOR |논리 연산자 XOR Exclusive OR(5/107)
Logical Operators - Exclusive OR XOR - 0. 논리합disjunction을 앞 장에서 살펴보았다. 논리합은 교집합과 유사한 개념으로, 명제 p, q가 모두 false일 때만 논리합 p∨q가 false가 된다. 이들의 진리표는 다음..
tomatolife.tistory.com
XOR
| x1 | x2 | y |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |

AND, OR과 달리, XOR는 직선으로 영역을 나눌 수 없다.
빨간 색 : True
파란 색 : False
다층 퍼셉트론
MultiLayer Perceptron, MLP

단층 퍼셉트론의 '선형성' 한계를 극복하기 위해
입력층, 출력층 사이에 층을 더 추가하여(Hidden layer) 다층 퍼셉트론을 만들게 된다.
그러다 Hidden layer가 2개 이상인 신경망을 Deep Nerual Network DNN이라고 한다.
가중치를 찾아가는 과정이 'training 학습' 단계에 해당하고,
머신 러닝에서는 손실 함수 loss function, optimizer 등을 사용한다.
그리고 training 시키는 Artifitial Neural Network가 Deep Neural Network 인 경우에,
Deep Learning이라고 한다.
신경망 Neural Network
활성화 함수 Activation Function
은닉층과 출력층의 뉴런에서 출력값을 결정하는 함수
'0이 될까, 1이 될까?'
이때, 활성화 함수는 반드시 비선형 함수여야 한다!
그래야만, 은닉층을 여러 번 추가하는 것이 유의미해지기 때문이다.
(활성화함수가 f(x) = Wx로 선형 함수인 경우, Hidden layer를 2개 추가하여도 y=W^3 * x = K * x로 선형 함수가 된다)
(선형 함수를 사용한 경우 'linear layer, projection layer'라고 한다)
종류에는 계단 함수, 시그모이드 함수, ReLU 함수, 항등 함수, Softmax 함수 등이 있다.
step function
def step(x):
return np.array(x > 0, dtype=np.int)
x = np.arange(-5.0, 5.0, 0.1) # -5.0부터 5.0까지 0.1 간격 생성
y = step(x)
plt.title('Step Function')
plt.plot(x,y)
plt.show()
sigmoid function

# 시그모이드 함수 그래프를 그리는 코드
def sigmoid(x):
return 1/(1+np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()

인공신경망의 학습 과정에서 시그모이드 함수의 문제점이 발생한다.
인공 신경망은 [1] 입력 신호에 대한 forward propagation 연산, 그 다음에는 [2] forward propagation 연산을 통해 나온 예측값과 실제값의 오차 계산 (loss function), [3] 그리고 loss를 미분 처리하여 gradient를 구하고, [4] 이를 통해 back propagation 을 수행하게 된다.
시그모이드 함수의 경우, [3] 단계에서 문제가 생기게 된다.
위 함수를 보면, 출력값이 0이나 1에 가까워질수록 미분값(기울기)가 0에 가까운 아주 작은 값이 나오게 된다. 그리하여 back propagation 과정에서 기울기가 잘 전달되지 않는다. 이를 vanishing gradient 문제라고 한다.
reLU function **
가장 인기있는 함수로
수식은 f(x) = max(0,x)이다.
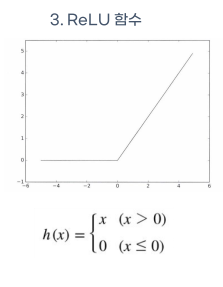
def relu(x):
return np.maximum(0, x)
x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.plot([0,0],[5.0,0.0], ':')
plt.title('Relu Function')
plt.show()-> 그러나 ReLU function은 입력값이 음수일 때는 기울기가 0이 되기 때문에 뉴런에 문제가 생김.
이를 보완하기 위해 'Leaky ReLU function'이 등장하였다.
3층 신경망 구현하기
구성 : 입력층(0층) 2개, 은닉층(1층) 3개, 은닉층2(2층) 2개, 출력층(3층) 2개로 구성

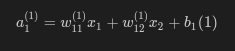
행렬의 내적을 이용하면, 1층의 가중치 부분을 행렬곱으로 나타낼 수 있다.
numpy를 이용해서 구현하면,
X = np.array( [1.0, 0.5] )
W1 = np.array( [0.1, 0.3, 0.5], [0.2, 0.4, 0.6] ] )
B1 = np.array( [0.1, 0.2, 0.3] )
A1 = np.dot(W1, X) + B11층에서의 활성화 함수 처리는, 그리하여 A1이 활성화함수를 처리하면 1이 되는지 보아야한다.
Z1 = sigmoid(A1)
print(A1) # [0.3, 0.7, 1.1]
print(Z1) # [0.57444252. 0.66818777, 0.75026011]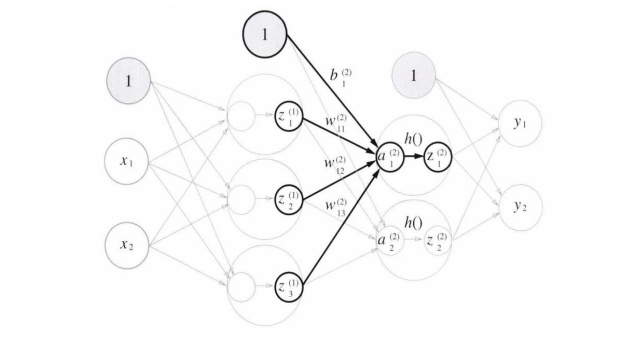
활성화 함수의 결괏값인 Z1과 가중치 W와의 내적을 하고, 이 결괏값을 편향 B2와 더하여 A2층을 구해준다.
즉, A2 = Z1 * W2 + B2
W2 = np.array( [ [0.1, 0.4], [0.2, 0.5], [0.3, 0.6] ] )
B2 = np.array( [0.1, 0.2])
print(Z1.shape) # (3,)
print(W2.shape) # (3, 2)
print(B2.shape) # (2,)
A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)
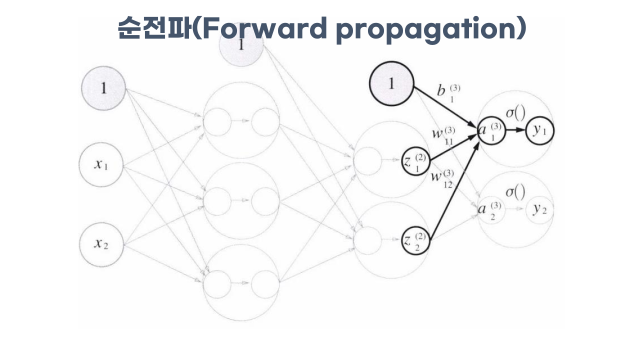
마지막 층에서 이전 hidden layer와는 다른 활성화 함수를 사용한다.
def identity_function(x): # 출력층 활성화 함수는 함등함수를 이용했습니다.
return x
W3 = np.array( [ [0.1, 0.3], [0.2, 0.4] ] )
B3 = np.array( [0.1, 0.2] )
A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3) # 혹은 Y = A3여기까지의 과정이 순전파 처리 과정이다.
손실 함수
손실 함수 loss function - 신경망이 학습할 수 있도록 해주는 지표
목표 : loss function의 값을 가장 작게 만드는 가중치 W를 찾는다.
loss function 의 종류

- 평균제곱오차 MSE Mean Squared Error
- 교차 엔트로피 오차 CEE cross entropy error
경사법
신경망의 손실함수를 작게 만드는 기법으로 함수의 기울기를 활용한다.
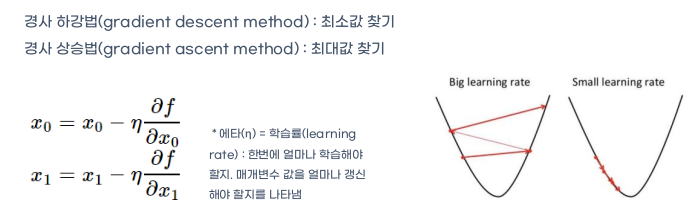
gradient method: 현 위치에서 기울어진 방향으로 일정 거리만큼 이동하여, loss function 의 값을 줄이는 방법
- 경사 하강법 gradient descent method
- 경사 상승법 gradient ascent method
learning rate : 한번에 얼마나 학습할 것인지를 결정함.
back propagation 오차역전파법
back propagation 알고리즘을 발견하면서 딥러닝 학계가 다시 활기를 띄게 된다.
(multi layer network의 학습이 가능하다는 뜻이기 때문이다.)
back propagation 알고리즘은, 에러를 output에서 가까운 쪽부터 뒤로(back) 전파(propagation)하는 것이다.
즉, 내가 구하고자 하는 target 값과, 나의 모델이 계산한 output의 에러(차이)를 계산한 뒤에,
그 오차값을 뒤로 전파하면서 노드의 변수(가중치 weight, 편향 bias)를 업데이트하는 알고리즘이다.
-> 이때, chain rule 미분 연쇄법칙을 이용해서 해결한다.
chain rule의 정의를 살펴보자.
| 함수 f, g가 있을 때, f, g가 모두 미분 가능하고 F = f(g(x)) = f g로 정의된 합성함수이면, F는 미분 가능하다. 이때 F' = {f(g(x))}' = f'(g(x))g'(x)이다. g(x) = t라고 하면, dy/dx = dy/dt * dt/dx가 성립한다. |
변수가 두 개일 때 chain rule은 어떻게 정의하는가?
| 이변수함수 z = f(x, y)에서 x = h(s, t), y = g(s, t)일 때, f, h, g가 모두 미분 가능하다면, z / s = (z /x ) * ( / s ) + (z / ) * ( / s ) (s에 대하여 z를 편미분하면, x와 y에 대해 연쇄법칙을 거친다) z / = (z /x ) * ( / ) + (z / ) * ( / ) |
참고 - https://kerpect.tistory.com/184
forward propagation을 통해 weight, bias를 모두 구한다.
그런 다음 weight, bias를 업데이트 해주기 위해 chain rule을 사용한다.
weight 하나가 에러 E에 얼마나 영향을 미쳤는가(기여도-> 기울기??)를 계산하는 것이다.
E에 대한 w_10^(1)의 기여도.
https://evan-moon.github.io/2018/07/19/deep-learning-backpropagation/
[Deep Learning 시리즈] Backpropagation, 역전파 알아보기
이번 포스팅에서는 저번 포스팅에 이어 에 대해서 알아보려고 한다. 앞서 설명했듯, 이 알고리즘으로 인해 에서의 학습이 가능하다는 것이 알려져, 암흑기에 있던 학계가 다시 관심을 받게 되었
evan-moon.github.io
계산 그래프의 역전파
참고 - https://deep-learning-study.tistory.com/16
계산 그래프 : 계산 과정을 그래프로 표현한 것이다.
그래프는 node, edge로 표현한다.
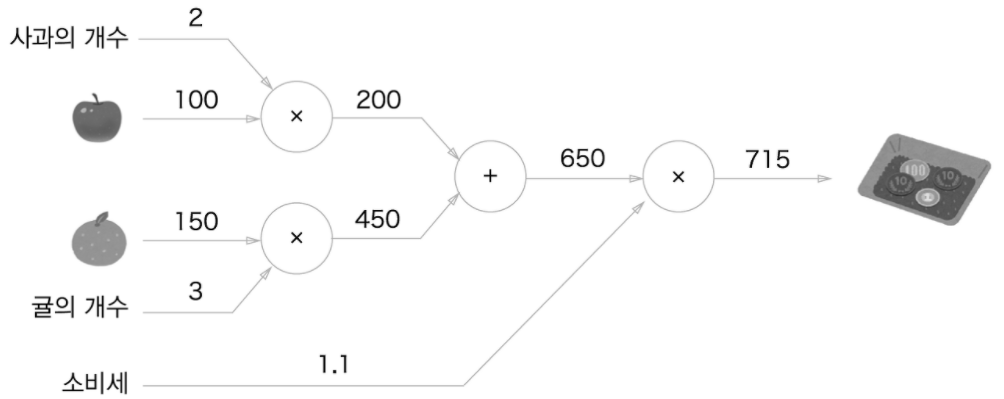
간단한 계산 그래프의 예시
덧셈 노드와 곱셈 노드가 있다.
계산을 왼쪽에서 오른쪽으로 수행하는 'forward propagation',
그리고 오른쪽에서 왼쪽으로 진행하는 'backward propagation'이 있다.
이 back propagation은 미분에서 중요한 역할을 한다.
덧셈 노드의 역전파 : 입력값을 그대로 다음 노드로 흘려 보낸다.
곱셈 노드의 역전파 : 상류의 값에 순전파 때의 입력 신호들을 서로 바꾼 값을 곱해 하류로 보낸다.
덧셈 노드의 역전파
z = x + y라고 할 때,
z = x + y의 미분은
∂z / ∂x = 1
∂z / ∂y = 1
따라서 상류에서 전해진 입력값의 미분값(∂L/∂z)에 1(∂z / ∂x 이자 ∂z / ∂y)을 곱하여 흘려보낸다.

class AddLayer:
def __init__(self):
pass # 덧셈 계층에서는 초기화가 필요 없습니다.
def forward(self, x, y):
out = x + y
return out
def backward(self, dout):
dx = dout * 1 # 상류에서 내려온 미분을 그대로 하류로 흘립니다.
dy = dout * 1
return dx, dy곱셈 노드의 역전파
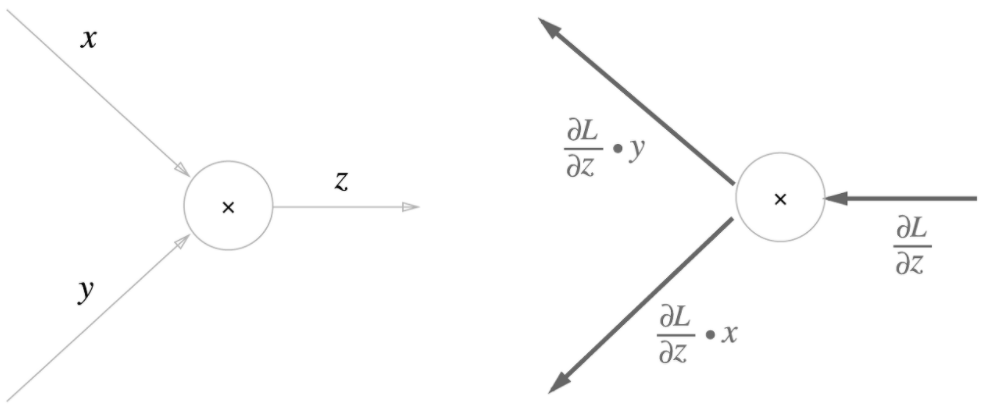
z = xy라는 식이 있을 때, 이 식의 미분은
∂z/∂x = y
∂z/∂y = x
이므로 계산 그래프는 x값에 입력값 * y를, y값에는 입력값 * x를 해서 하류로 흘려보낸다.
class MulLayer:
def __init__(self): # 변수 x와 y초기화
self.x = None
self.y = None
def forward(self, x, y):
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout): # dout은 상류에서 넘어온 미분(dout)
dx = dout * self.y # x와 y를 바꾼다.
dy = dout * self.x
return dx, dy학습 관련 기술들
매개변수 갱신
optimization
- loss function을 최대한 작게 하는 weight, bias를 찾고자 한다.
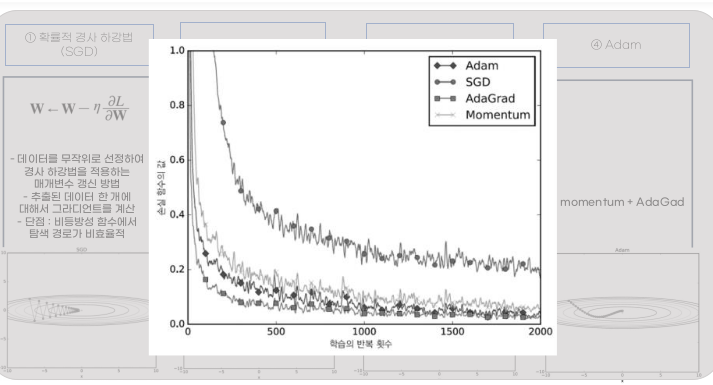
- 종류에는 SGD, momentum, AdaGrad, Adam 등이 있다.

확률적 경사 하강법 SGD Stochastic Gradient Descent
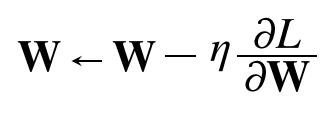

가장 간단한 학습 최적화 방식
step 1. loss function (L) 의 gradient를 구한다.
∂L / ∂W (weight에 대한 loss function의 변화량/기울기)
step 2. gradient에 learning rate (η)만큼을 곱한다.
step 3. 현재 W에 빼주어 이를 새로운 가중치로 계산한다.
step 4. 반복
(+) 단순, 구현하기 쉬움
(-) 비효율적
Momentum
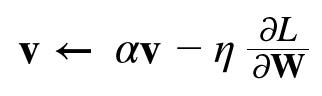


Stochastic Gradient Descent SGD 기법에 속도(v) 개념을 적용한다.
'기울기 방향으로 힘을 받으면, 물체가 가속된다(a)'는 법칙을 알고리즘에 적용한 것이다.
v라는 속도 항에 기울기 값이 누적되고,
누적된 값이 가중치 갱신에 영향을 준다.
AdaGrad
Adaptive Gradient Algorithm


학습을 진행하면서 learning rate를 점차 줄여나가는 기법을 사용한다.
(최적점에 가까워질수록 각 매개변수에 맞게 학습률을 줄임)
h는 h + (∂L / ∂W)^2
학습이 진행됨에 따라 기울기를 거듭하여 거대준다.
매개변수를 갱신할 때 h의 제곱근을 나누어 학습률을 조정한다.
h는 계속해서 커지기 때문에, 학습을 하면서 learning rate가 감소하는 경향을 보이나,
이전에 가중치가 갱신되었던 크기에 반비례하여 학습률이 결정되게 된다.
Adam

가중치의 초깃값
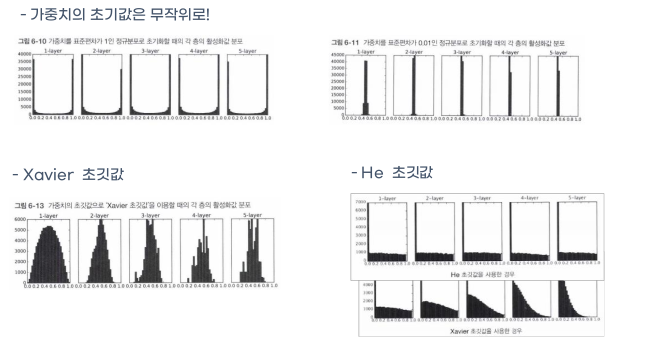
가중치의 초깃값은 무작위로 정한다.
Xavier 초깃값 제ㅣ비어?
앞 계층의 노드가 n 개일 때 가중치 초깃값을 표준편차가 1/√n 인 정규분포를 갖도록 설정하는 것이
Xavier 초깃값 (Xavier Initialization) 입니다.
He 초깃값 허?
He 초깃값은 활성화함수로 ReLU를 사용할 때 특화된 가중치 초기값입니다.
앞 계층의 노드가 n개일 때, 표준편차가 √(2/n) 인 정규분포를 사용합니다.
배치 정규화

Batch Normalization
- 학습하는 과정을 전체적으로 안정화시키는 방법
- 높은 학습률, 빠른 속도
- 초기값 영향 감소
- 규제의 효과 > 오버피팅 억제
- 감마 scale, 베타 shift 조정이 가능
- 비선형성 유지, saturation 현상 조절 가능함.
바른 학습을 위해
오버피팅 : 매개 변수가 많고, 표현력이 높거나 훈련 데이터가 적을 때 발생한다.
이때
가중치 감소 - 큰 가중치에 대해 큰 패널티 부과
드롭 아웃 - 뉴런을 임의로 삭제하며 학습
사용 가능함.
적절한 하이퍼파라미터 값 찾기
- train 데이터 : 매개변수 학습
- valid 데이터 : 하이퍼 파라미터 성능 평가 <- 하이퍼파라미터의 최적값을 찾음.
- test 데이터 : 신경망의 범용 성능 평가
'Data Science > AI' 카테고리의 다른 글
| CNN Convolution Neural Network 에 대해 알아보자 | computer vision, filter, LeNet, AlexNet (0) | 2021.09.25 |
|---|---|
| Deep Learning - DNN에 대해 알아보자 | ANN, DNN (0) | 2021.09.25 |
| NLP - attention (0) | 2021.09.24 |
| What is Spark Streaming? | RDD, SparkStreaming, DStream, Sparkconfig | 작성 중 (0) | 2021.09.16 |
| What is Git and GitHub? | 깃, 깃허브 이용법 (0) | 2021.08.29 |