숙명여대 학점교류로 듣는 자료구조
day 7. 2021.12.30
overflow handling
- open addressing - address is not fixed
linear probing : 선형 탐색법
quadratic probing : 2차
rehashing : 재해싱
원래 들어가야 하는 버킷인 home bucket이 아니라, 다른 주소에 저장하는 것을 허용하는 방식이다.
- chaining
* linear probing : 선형 조사법
버킷에 오버플로우가 발생하면, 다음 번 빈 버킷을 찾아 저장한다.
suppose a hash table is represented in one-dimensional array
h = hashing(26)
* initialization of the hash table
allow overflows and collisions to be detected
all buckets to empty string(Null)
class hashing:
def __init__(self, size):
self.size = size
self.table = [None]*size
def hf(self, key):
# 버킷 주소로 쓴다.
# 해싱의 원리임
total= 0
for s in key:
total += ord(s)
return total % self.sizeOverflow handling
* hashing elements in hash table
b = 13, s = 1
hash function
sum of ASCII codes % b
최종적으로 다시 나누어준다.
collision 일어남 (12가 겹치는 현상)
* linear probing
find the next empty bucket when a new element is mapped into a full bucket
hash table : 13 buckets, bucket size = 1 slot / bucket
남의 홈 버켓에 넣어준다.
0번이 홈 버켓이 아닌 애가 들어오면, 다시 다른 애에 넣어준다.
function을 찾아내고 싶을 때, 찾아보아도 없게 됨.
다시 참조할 때에도 효율적이지 않다.
* 4 cases when hash table is examined by linear probing
ht[(f(x)+j) % TABLE_SIZE], where 0<=j<TABLE_SIZE]
순환하면서 다른 위치에 갈 수 있다.
Case 1 : the bucket already contains the key x
simply report a duplicate identifier
Case 2 : the bucket is empty
insert a new element into it
Case 3 : the bucket contains a key other than x
overflow occured; proceed to examine the next bucket
Case 4 : returnint to the home bucket
ht[f(x)] (j=TABLE_SIZE)
the home bucket is being examined for the second time and all remaining buckets have been examined
report an error condition and exit
* characteristics of linear probing
identifiers tend to cluster together ; 덩어리진다.
이 근처에 정의된 단어는 다시 그 근처에 정의되고, 이것 때문에 효율이 떨어진다.
cause to increase the search time to O(n) rather than O(1)
ex) hash the c built in function names into a 26-bucket hash table
{acos, atoi, char, define, exp, ceil, float, cos, atol, floor, ctime}
b = 26, s = 1
* linear probing
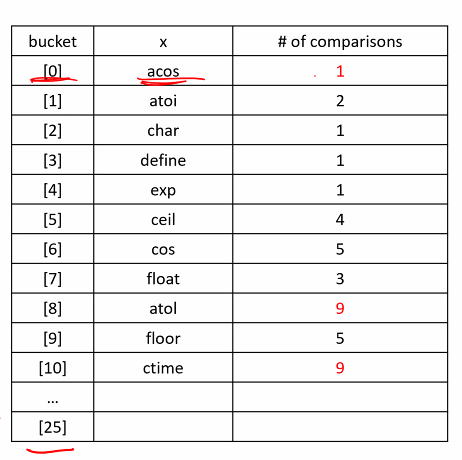
이것이 다 클러스터임.
어떻게 개선할 것인가?
Overflow Handling
* Identifier clustering by linear probing
tend to merge
as more identifiers enter the table, the cluster gets bigger
* solutions of clustering/overflow
use open addressing
: quadratic probing
: random probing
: rehashing
Quadratic probing 2차 조사법
바로 다음에 비어있는 곳이 아니라,
ht[f(x)], ht[(f(x)+-i^2)%b]
ht[f(x)], ht[f(x)+1], ht[f(x)-1], ht[f(x)+4], ht[f(x)-4], ht[f(x)+9], ht[f(x)-9]
Rehashing
미리 hashing function을 여러 개 준비해둔다
f1이 실패하면, f2를 사용한다. 다시 실패하면 f3 이용한다.
반대로 f3를 해서 들어가면, 이 값을 읽어올 때에도 거꾸로 f1, f2, f3을 모두 시도해보아야 한다.
안 좋은 점..
Chaining = 오버 플로우가 생기지 않도록 하는 방법
Fundamentally avoid bucket overflow
one linked list per one bucket
each list has all synonyms
requires a head pointer for each chain
as the length of chain increases, search time approaches O(n) and loses the benefit of hashing search
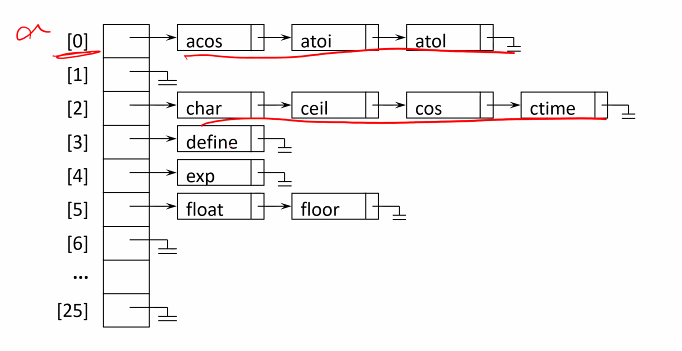
overflow는 절대 생기지 않는다.
그러나 내부에서 순차탐색을 하는 것이 비효율적임.
아이디어는 좋으나, 순차탐색이 내부에서 발생할 수 있으므로 적절히 사용하여야 한다.
시험 안내
답만 쓰라고 하면, 답만 써야한다(숫자로)
'Computer Science > 자료구조' 카테고리의 다른 글
| 자료구조 | Permutations, N Queens problem | backtracking (0) | 2021.12.31 |
|---|---|
| 자료구조 | 자료구조 개념 및 구현 연습문제 풀이 - 3장 | 숙명여대 학점교류 (0) | 2021.12.31 |
| 자료구조 | Binary Search | Search (0) | 2021.12.29 |
| 자료구조 | Sequential Search | Search (0) | 2021.12.29 |
| 자료구조 | Deque Double Ended Queue | Linked List (0) | 2021.12.29 |