숙명여대 학점교류로 듣는 자료구조
day 11. 2022.1.5. 수요일
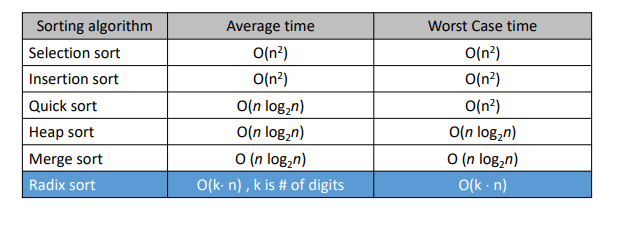
정렬
insertion sort => quadratic
------ shell sort => faster than quadratic
quick sort
heap sort
merge sort
radix sort
Insertion sort
If n <= 1, already sorted. So, assume n>1
a[0:n-2] is sorted recursively
a[n-1] is inserted into the sorted a[0:n-2]
complexity is O(n^2)
usually implemented non-recursively

Insert a number to the sorted list
n 앞까지는 모두 정렬되어있다고 가정하고, n번째 원소를 알맞은 위치에 삽입한다.
class InsertionSort:
def __init__(self, num):
self.num = num
self.size = len(num)
print("Insertion Sort", self.num)
def __str__(self):
for i in range(self.size):
print("%2d " % self.num[i])
def sort(self):
for i in range(1, self.size):
pivot = self.num[i]
j = i-1
while j >= 0 and pivot < self.num[j]: # j를 밀어내야한다
self.num[j+1] = self.num[j]
j-= 1
self.num[j+1] = pivot
print(self.num)
num = [13, 25, 9, 12, 34]
c = InsertionSort(num)
c.sort()이미 정렬된 상태에서 하면, 시간 복잡도가..
average는 O(n^2)이다.
=> quadratic time에서 벗어나기 위한 첫 시도 : shell sort
Shell sort

Invented by Donald Shell in 1959
1st algorithm to break the quadratic time barrier
a sub quadratic time algorithm : between linear and quadratic
shell sort improves on the efficiency of insertion sort by comparing elements that are distant rather than adjacent element in an array
when n elements are to be sorted, the first gap will be (n/2) or (n/2)+1
the gap decreases by half in each phase until gap is 1
=> gap이란, 비교하는 원소
=> 비교하는 원소끼리 insertion sort를 해준다.
after each phase and some gap hk, for every i, we have all elements spaced hk apart are sorted
the file is said to be hk-sorted
=> 이렇게 해서 gap만큼 떨어진 원소 사이에는 sorted 되어있게 된다.
다음에는 갭을 반으로 나누어서 ..
gap만큼 떨어진 원소들끼리 insertion sort를 해준다.
떨어져있는 원소 간에 insertion sort를 해주는 것이 아이디어다.
갭이 홀수일 때 성능이 더 좋다.

gap = 5, 3, 1로 줄이면서 insertion sort를 거듭하여 진행한다.
class ShellSort:
def __init__(self, num):
self.num = num
self.size = len(num)
print("Shells Sort", self.num)
def __str__(self):
for i in range(self.size):
print("%2d " % self.num[i])
def sort(self):
n = self.size
gap = n//2
while gap > 0: # 갭을 정해준다
if gap % 2 == 0: gap += 1 # 갭을 홀수로 정한다
for i in range(gap, n): # gap에서 self.size까지
h = 1
while i * h < n:
j = i*h # gap만큼 증가한 index를 위한 변수
temp = self.num[i*h]
while j >= gap: # insertion sort
if temp < self.num[j-gap]: # 정렬 필요
self.num[j] = self.num[j-gap]
else: break # 이미 정렬된 것
j -= gap
self.num[j] = temp
h += 1
print(gap, self.num)
gap //= 2
num = [13, 25, 9, 12, 34]
c = ShellSort(num)
c.sort()
shell sort의 의의
Advantage
faster than O(n^2), slower than O(n)
Experiments suggest something like O(n^3/2) : average = sub-quadratic time
5 times faster than buble sort and a little over twice as fast as the insertion sort
good choice for sorting lists of less than 5000 items
Disadvantage
complex algorithm
slower than the merge, heap, and quick sorts
=> 시험에 잘 나옴 :) 주의***
=> 정렬에서 시간 복잡도 잘 알고 있어야 한다.
Quick sort
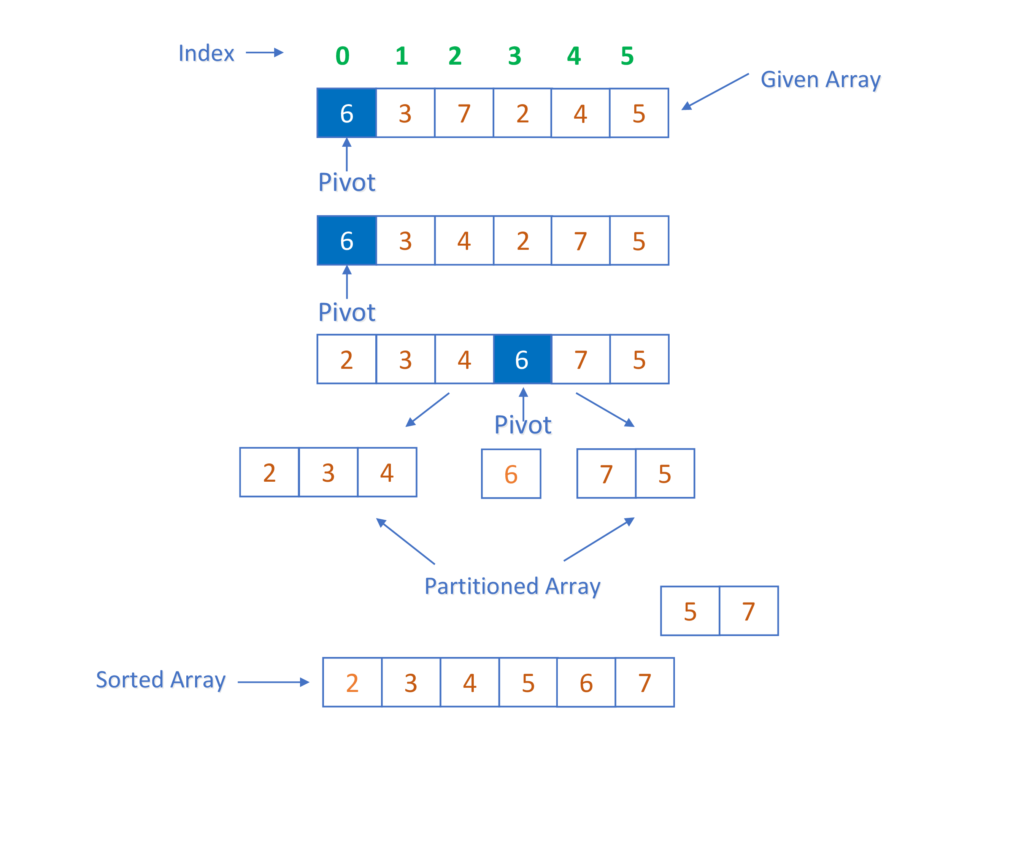
when n <= 1, a list is sorted
when n > 1, select a pivot element out of n elements
partition the n elements into 3 segments left, middle, and right
the middle segment contains only the pivot elements
=> left , right 부분을 quick sort로 정렬해준다
All elements in the left segment are < pivot
All elements in the right segment are > pivot
sort left and right segments recursively
the answer is sorted left segment, followed by middle segment followed by sort
choice of Pivot
적정하게 분할해주는 pivot을 선정해주어야 한다.
분할이 일어나지 않을 때까지 쪼개야하니까 반씩 쪼개는 것이 가장 효과적이다.
the pivot is a leftmost element in list that is to be sorted
when sorting a[6:20], use a[6] as the pivot
randomly select one of elements to be sorted as the pivot
when sorting a[6:20], generate a random number r
Median of Three rule
from the leftmost, middle, and rightmost elements of the list to be sorted, select the one with median key as the pivot
셋 중에 중간값을 pivot 값으로 쓴다.
when the pivot is picked at random or by the median-of-three rule, we first swap the leftmost element and the chosen pivot to use the identical sorting code in textbook
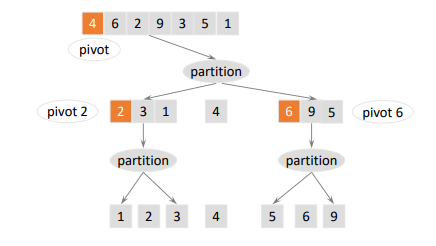
step 1. based on a pivot, partition elements into small and large number segments
step 2. repeat step 1. until when a partition is no longer possible
def QuickSort(A, start, end):
if start >= end:
print(A[start])
return
m = Partition(A, start, end)
QuickSort(A, start, m-1)
QuickSort(A, m+1, end)
def Partition(A, start, end):
pass
Partition Method : In-place partition
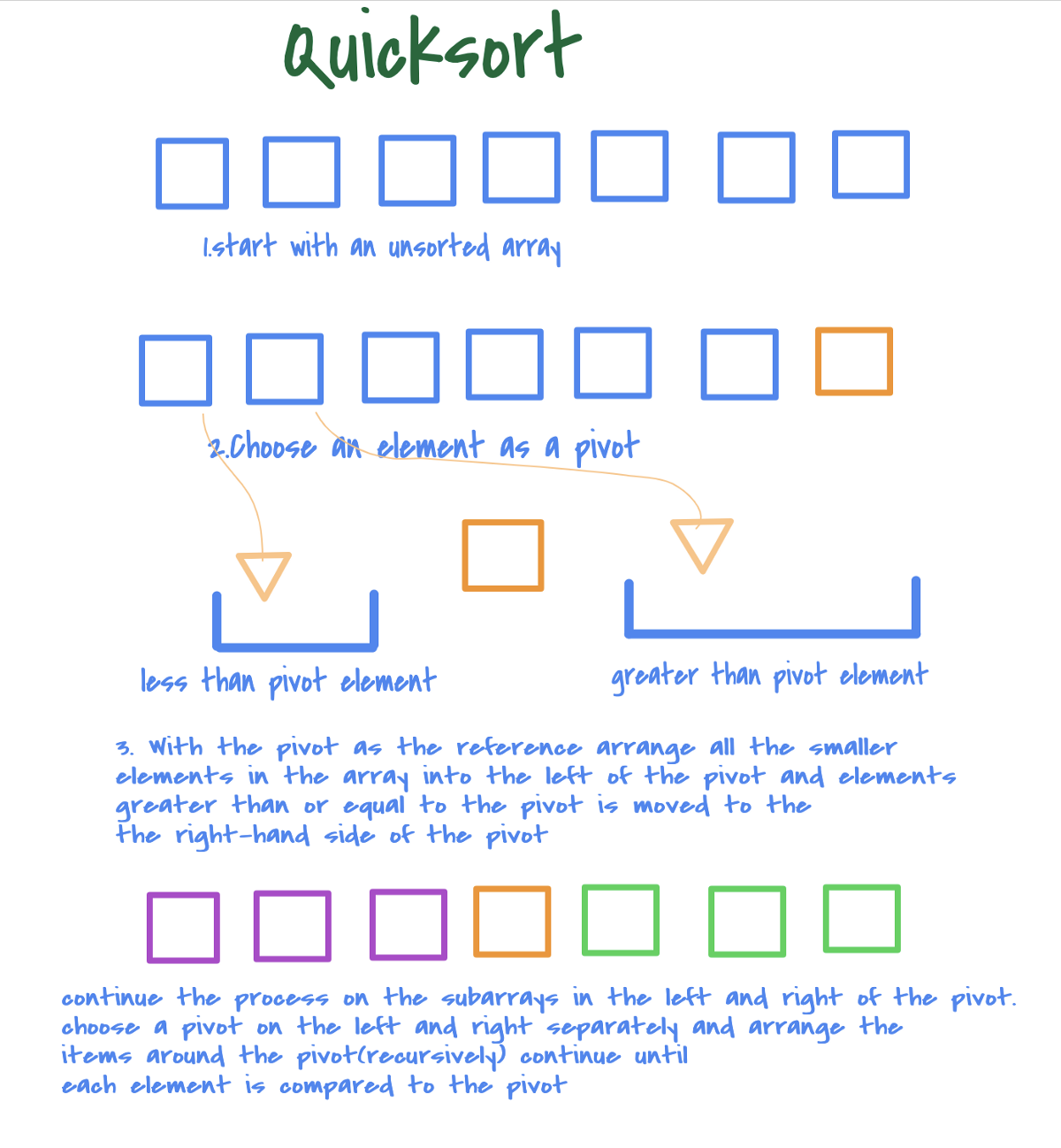
i++ until finding a bigger number than pivot
j-- until finding a smaller number than pivot
swap(list[i], list[j]) and repeat the above as long as i < j
if i >= j, swap A[j] with the pivot
=> i >= j가 되면, pivot과 j의 위치를 바꾸어준다.
In-place partition
pivot = A[0]
i++ and j-- until finding bigger/smaller number than pivot, respectively
if suck i and j are found, swap(A[i], A[j])
repeat this as long as i<j
if i>=j, swap(A[j], pivot)
and then, call Quicksort(0, j-1) and Quicksort(j+1, 9), recursively
pivot이 이동할때마다 배열의 내용을 출력해보면 정확하게 알 수 있다.
class QuickSort:
def __init__(self, num):
self.num = num
self.size = len(num)
print("Quick Sort", self.num)
def swap(self, a, b):
self.num[a], self.num[b] = self.num[b], self.num[a]
def sort(self, left, right):
if left < right:
i = left
j = right + 1
pivot = num[left]
while True:
while True:
i+= 1
if i > right or num[i] >= pivot:
break
while True:
j -= 1
if j < left or num[j] <= pivot:
break
if i < j:
num[i], num[j] = num[j], num[i]
else:
break
num[left], num[j] = num[j], num[left]
if left != j:
print(self.num)
self.sort(left, j-1)
self.sort(j+1, right)
num = [26,5,37,1,61,11,59,15,48,19]
s = QuickSort(num)
s.sort(0, len(num)-1)
performance analysis
best, worst, average를 알아두어야 한다.
average time complexity : O(nlogn) => 관건은 pivot
worst case time complexity : O(n^2)
subfile1 = size0
subfile2 = sizen-1
Merge sort
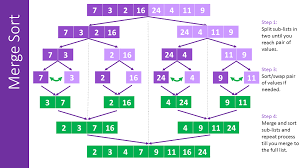
partition the n>1 elements into two smaller segments
first ceil(n/2) elements define one segment
remaining floor(n/2) elements define the second segment
each of the two smaller segments is sorted recursively
the two sorted segments are combined using a process called merge
각각의 segment를 merge sort해준다.
n이 한개가 될 때까지 쪼갠 뒤에, 더이상 쪼개지 않는다.
Merge two sorted list
예시
a = (2,5,6)
b = (1,3,8,9,10)
c = ()
a = (5,6)
b = (3,8,9,10)
c = (1,2)
a = (5,6)
b = (8,9,10)
c = (1,2,3)
a = () => 하나가 empty가 되면, 나머지 원소에 추가해주고 끝낸다
b = (8,9,10)
c = (1,2,3, 5,6)
a = ()
b = (8,9,10)
c = (1,2,3,5,6,8,9,10)
when one of A and B becomes empty, append the other list to C
O(1) time needed to move..
merge를 하려면, 각 리스트가 정렬이 되어있어야 한다.
각각을 정렬해준 뒤에, 두 리스트를 합병해준다.
알고리즘 divide
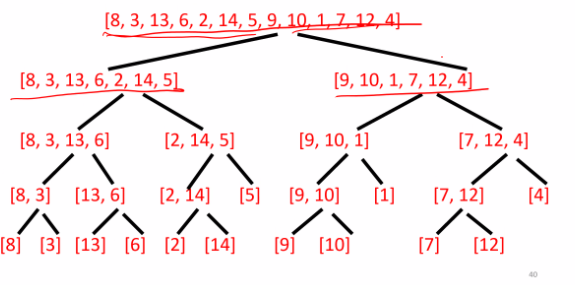
1. 리스트를 반으로 분할해준다
2. 리스트를 반으로 분할해준다
3. 리스트를 반으로 분할해준다.
...
5. 그렇게 원소를 1개로 모두 쪼개어준다.
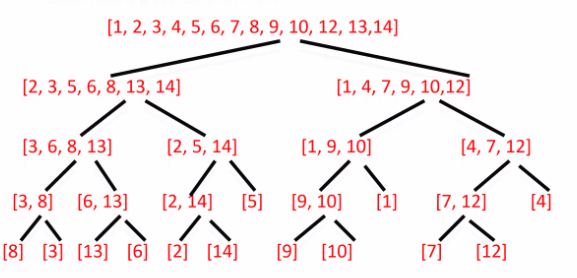
conquer
1. 말단에서부터 merge해주며 올라간다
like 8, 3= > 3, 8 / 13, 6 => 6, 13
그 다음에는 더 큰 단위로 merge해준다.
like 3,6,8,13 / 2,5,14 => 2,3,5,6,8,13,14
left를 먼저 호출해준다
Time Complexity
downward passing
- divied large instances into small ones
- O(n) total time at all nodes
upward passing
- merges of pairs of osrted list
- O(n) time for merging at each level that has a nonleaf node
- Number of levels is (logn개의 레벨이 있다)
- Total time is O(nlogn)
Total
n + nlogn = O(nlogn)
class MergeSort:
def __init__(self, num):
self.num = num
def mergesort(self, left, right):
if right > left:
mid = (left + right) // 2 # 분할
self.mergesort(left, mid) # sort
self.mergesort(mid+1, right) # sort
self.merge(left, mid+1, right) # merge
def merge(self, left, mid, right): # 1st = [left..mid-1] 2nd = [mid..right]
pos = left
left_end = mid - 1
n = right - left + 1
temp = [None] * self.size
while left <= left_end and mid <= right:
# 앞 부분을 비교해서 작은 요소를 먼저 넣는다
if self.num[left] <= self.num[mid]:
temp[pos] = num[left]
pos = pos + 1
left = left + 1
else:
temp[pos] = num[mid]
pos += 1
mid += 1
while left <= left_end:
temp[pos] = num[left]
left += 1
pos += 1
while mid <= right:
temp[pos] = num[mid]
mid += 1
pos += 1
for i in range(n):
# temp를 num 배열에 복사해준다
self.num[right] = temp[right]
right -= 1
num = [40,15,34,29,3,10,9,17,37]
s = MergeSort(num)
s.mergesort(0, len(num)-1)
Natural Merge Sort
이미 정렬이 되어있는 경우는?
initial sorted segments are the naturally occurring sorted segements in the input
ex input = [8,9,10,2,5,7,9,11,13,15,6,12,14]를 원소 1개 단위로 쪼개는 것이 아니라
[8,9,10][2,5,7,9,11,13,15], [6,12,14]로 쪼갠다.
merge passes suffice
segment boundaries have a[i] > a[i+1]
Radix Sort 기수 정렬
a kind of distributive sort
repeat the following 3 steps
non-comparitive sorting
1) comparison
LSD Least Significant Digit
MSD Most Significant Digit
2) distribution
3) merge
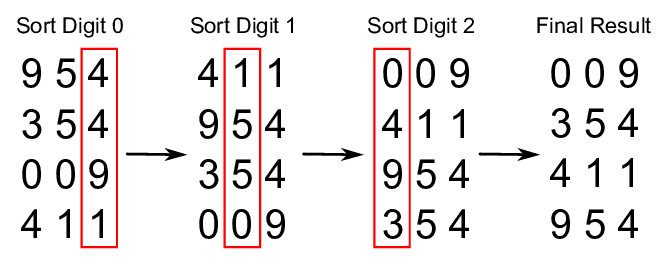
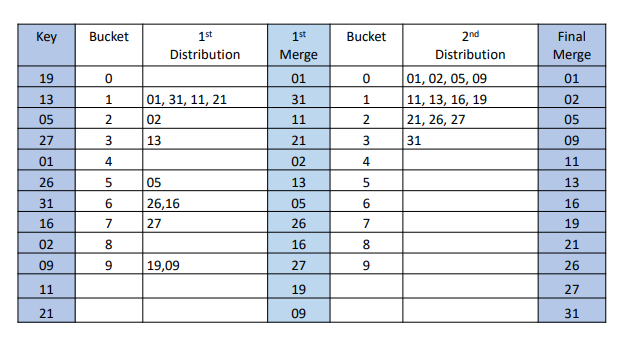
1의 자리를 보고, 해당하는 방(Bucket)으로 이동시켰다.
10의 자리를 보고, 다시 두번째 버킷으로 보낸다.
마지막으로 정렬을 해준다.
방법은 key를 직접 비교하지는 않아도 된다는 장점이 있다.
Radix sort's efficiency is O(k*n) for n keys which have k or fewer digits
Radix sort is non-comparative integer sorting algorithm that requires a positional notation
'Computer Science > 자료구조' 카테고리의 다른 글
| 자료구조 | Graphs | 숙명여대 학점교류 (0) | 2022.01.06 |
|---|---|
| 자료구조 | Binary Search Trees | 숙명여대 학점교류 (0) | 2022.01.06 |
| 자료구조 | 이진 트리 구현 (python) | Trees (0) | 2022.01.04 |
| 자료구조 | 정렬 Sorting | 숙명여대 학점교류 (0) | 2022.01.04 |
| 자료구조 | Binary Trees - 2강 | 숙명여대 학점교류 (0) | 2022.01.04 |