숙명여대 학점교류로 듣는 자료구조
day 12. 2022.1.6. 목요일
Binary Search Trees
Binary search Trees
Balanced binary search trees : AVL Tree
heap
provides a good performance of O(log2n) only when handling the root
for searching other item than the root, it takes O(n) time
why binary search tree is necessary
requires O(log2n) for any item, which is proportional to tree height (h)
=> 이진 탐색을 트리로 구현한 것
Binary search tree
assume no overlapping elements in tree
def)
* the root > left sub-tree nodes
* the root < right sub-tree nodes
* left & right sub-trees also must be binary search tree
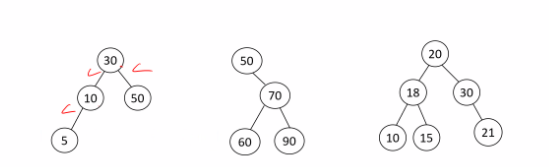
binary search tree의 조건
반복문과 재귀문으로 구현할 수 있다.
재귀문 버전 => O(log2n) + recursion overhead
def rBST(root, key):
if not root: return None
if key == root.data: return root
if key < root.data:
return rBST(root.left, key)
return rBST(root.right, key)반복문 버전 => O(log2n)
def iBST(root, key):
while root:
if key==root.data: return root
if key < root.data:
root = root.left
else:
root = root.right
return None수를 주면, 구성하는 것은 쉽다
Insertion Algorithm
before inserting a node, it should confirm whether there is no overlapping node.
if overlapped, insertion fails
otherwise, attach a new node (35) to the last item compared (40)
왼쪽, 오른쪽으로 root와 크기를 비교해가면서 내려가는데,
만약 노드가 중복인 요소가 있다면, 거절 아니라면 위치시키기
BST는 흥미롭네 ㅎㅎ >0<
overlap_check()
if tree is empty, or any overlapped node exists, NULL is returned
otherwise, a node searched lastly will be returned
time complexity : O(log2n)
search : O(log2n)
insert : O(1)
def insert(self, item):
node = Node(item)
if not self.tree:
self.tree = node
else:
temp = self.tree
# 상위 노드
prev = None
while True:
# 직전 노드 저장해두기
prev = temp
# item 현재 삽입하려는 item이
# prev보다 작다면,
# left로 내려가기
if item < prev.data:
temp = temp.left
if not temp:
# 만약에 left 값이 비어있다면,
# 노드를 넣어준다 :)
prev.left = node
return
# 비어있지 않다면 다시 내려가주어야 한다.
# right로 내려가기
elif item > prev.data:
temp = temp.right
if not temp:
# 만약에 right 값이 비어있다면,
# 노드를 넣어준다 :)
prev.right = node
return
# item == prev.data => 중복이므로 pass
else: return만약에 empty가 아니라면? empty인 곳에 붙여준다
중간 시험 점수가 높으니, 과제 점수가 변별력이 있을 것이다.
delete Algorithm
=> delete를 해도 BST 구조가 유지되어야 한다.
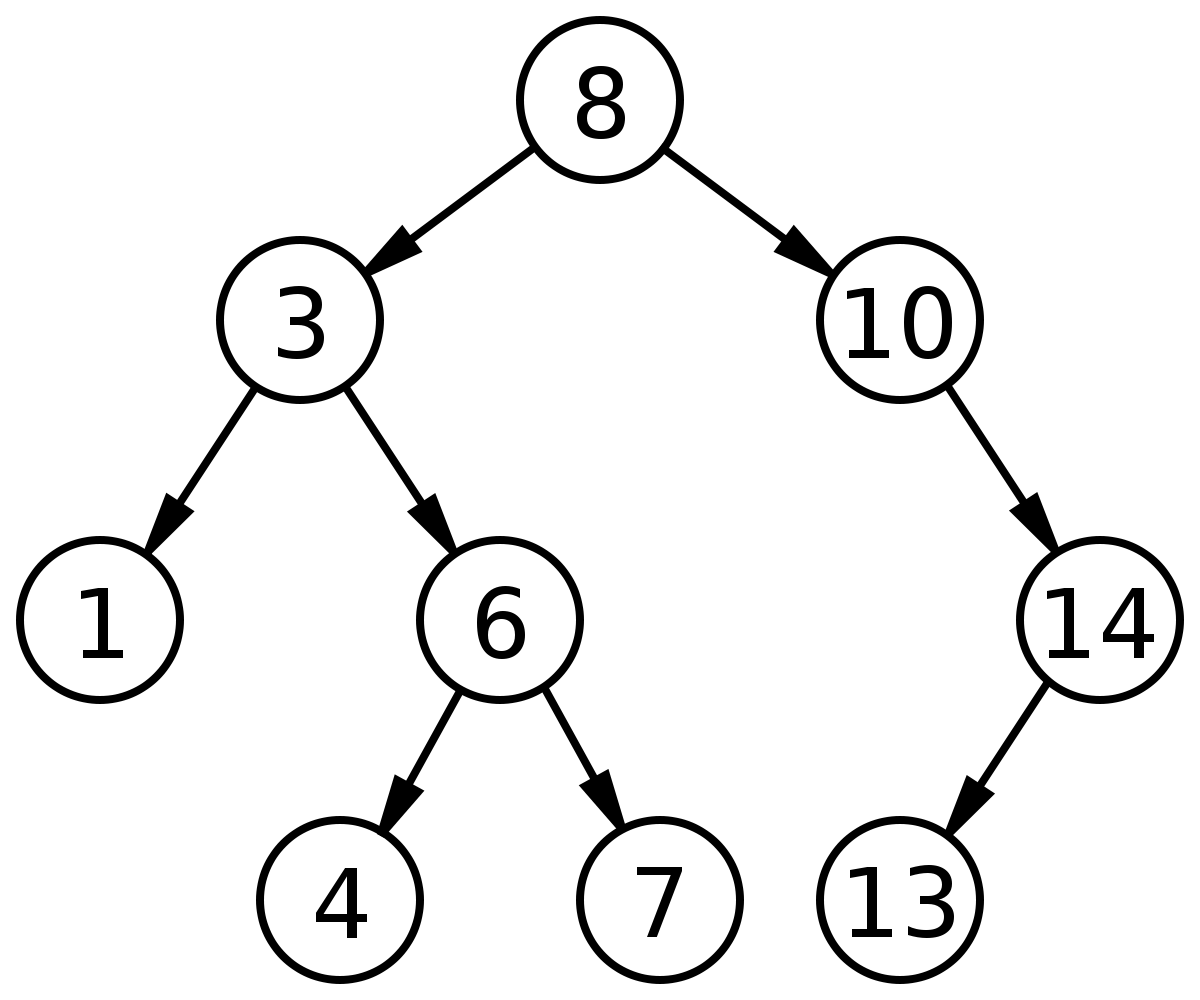
* deleting a leaf node
assign NULL to the parent's link
* deleting a node with one child
assign its child to the parent's link
* deleting a non-leaf node with two children
choose either the max node in left sub-tree or the min node in right sub-tree which can reduce the tree height
substitutes chosen node for the node to be deleted
rebuild the sub-tree for BST
two-child case일 때는 삭제하고나서도 BST가 유지되려면, 왼쪽 sub tree의 max 값이 오거나
오른쪽 sub tree의 min 값이 와줘야 한다.
Time complexity => O(log2n)

더 나은 방법은 무엇일까?
70만 올라가면, 성능은 높이에 비례한다. 근데 70이 가면 높이가 그대로다.
BST가 효율적인 형태가 되기 위해서는, 높이를 효과적으로 줄여야 함 ㅇㅎㅇㅎ
임의로 left의 max로 한다고 고정해둔다.
def find_delete(self, item):
# item을 삭제하여라
# 재귀 함수 작동을 위함
self.tree = self.delete_node(self.tree, item)
def delete_node(self, node, item):
if node is None: return None
if node.data > item:
# 탐색을 왼쪽 subtree로 이어간다
node.left = self.delete_node(node.left, item)
return node
elif node.data < item:
# 탐색을 오른쪽 subtree로 이어간다
node.right = self.delete_node(node.right, item)
return node
else: # 실제로 삭제하는 경우
if node.left is None: # 단말 노드이거나 one child인 경우
return node.right # None이거나, right subtree를 주면 된다.
elif node.right is None: # 단말 노드이거나 one child인 경우
return node.left # None이거나, left subtree를 주면 된다.
elif node.left is None and node.right is None:
return None
else:
# two child
left_max = self.find_max(node.left) # left subtree의 max를 임의로 정한다.
node.data = left_max.data
# 또다른 삭제 연산을 발생시킨다
node.left = self.delete_node(node.left, left_max.data)
return node
최댓값을 찾아보자
def find_max(self, root):
# BST 이므로 최댓값은 최대한 우측으로
# 최솟값은 최대한 좌측으로 이동해주면 된다!
if not root: return None
node = root
while node.right:
node = node.right
return node
time complexity
average : O(log2n)
Worse : O(n) - skewed tree
best case : O(log2n) - balanced binary search tree
Binary Balanced Search Tree
if height of binary search tree is n
insertion, deletion can be O(n) in the worst case
good to keep a tree height small
minimum height of a binary tree with n nodes : O(log2n)
goal
- keep the height of a binary search tree O(log2n)
balanced binary search trees
AVL tree, 2-3-4 tree, red-black tree
suggestion
every node must have left and right subtrees of the same height
hard to satisfy this except for complete full binary trees
our choice
for each node, the height of the left and right subtrees can differ at most 1
Balance Factor
balance factor (BF) of a node
: height (left subtree of the node) -
AVL Tree
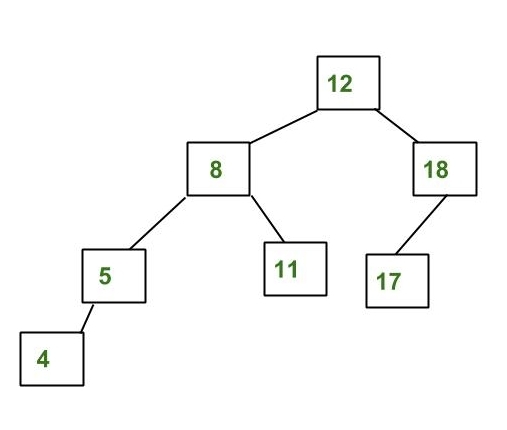
사람 이름 : Adelson-Velskii and Landis, 1962
AVL tree is a binary search tree in which
for every node in the tree, the height of the left and right sub-trees differ by at most 1
height 0
height 2
인 경우에는 AVL 조건 위배
Balance Factor
BF balance factor of a node : height (left subtree of the node) - height(right subtree)
avl tree: BF of all node should be 1, 0, -1
* height (empty sub tree) = -1
(8) = 0 - (-1) = 1
AVL tree with min number of nodes
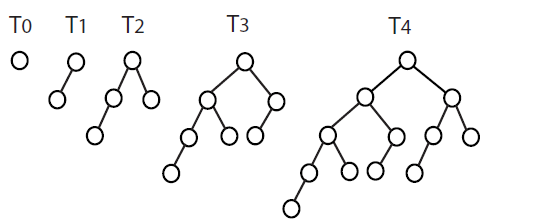
Nh = minimum # of nodes in a tree of height h
최소 구성원(?)
N0 = 1
N1 = 2
N2 = 4
N3 = N2+N1+1 = 7
Nh = Nh-1+Nh-2 + 1
thus searching on an AVL tree will take O(log2n) time

Insertion in AVL Tree
basically follows insertion strategy of binary search tree
but may cause violation of AVL tree property
restore the destroyed balance condition if needed

after an insertion, only nodes that are on the path from the insertion point to the root might have their balance altered
because only those nodes have their subtrees altered
rebalance the tree at the deepest, such node guarantees that the entire tree satisfies the avl property
After an insertion, only nodes that are on the path from the insertion point to the root might have their balance altered •
Because only those nodes have their subtrees altered •
Rebalance the tree at the deepest, such node guarantees that the entire tree satisfies the AVL property
Rebalance of AVL tree
rebalance of AVL tree are done with simple modification to tree, known as rotation
insertion occurs on the outside
Denote the node that must be rebalanced α
• LL case : an insertion into the left subtree of the left child of α
• LR case : an insertion into the right subtree of the left child of α
• RL case : an insertion into the left subtree of the right child of α
• RR case : an insertion into the right subtree of the right child of α
• Rebalance of AVL tree are done with simple modification to tree, known as rotation
• Insertion occurs on the "outside"
• left-left or right-right cases
• Is fixed by single rotation of the tree
• Insertion occurs on the "inside"
• left-right or right-left cases
• is fixed by double rotation of the tree
First, insert a new key as a new leaf just as in ordinary binary sear ch tree
• Check BF of each node in the path between a new node and the root.
• If BF is OK(0, -1, +1), proceed to parent(x)
• If not, restructure it by doing either a single rotation or a double rotation
• Note
• once we perform a rotation at a node x,
we won’t need to perform any rot ation at any ancestor of x.
single rotation - LL insertion
single rotation - RR insertion
example - AVL tree construction

BST insertion으로 넣는다.
LL case -> single rotation
RR case -> single rotation
계속 넣어주되, LL, RR 발생시 single rotation 해주기
RL case -> double rotation 해주어야 한다.
Double Rotation (left-right insertion)
Facts
- a new key is inserted in the subtree B or C
k3-k1-k2 forms a zig-zag shape
solution
- the only alternative is to place k2 as the new root ㅇㅎ
Double Rotation (right-left insertion)
facts
- the new key is inserted in the subtree B or C
- the AVL-property is violated at k1
- k1-k3-k2 forms a zig-zag..
15한테 14를 주어야 한다. child로..
subtree 관계를 잘 살펴보아야 한다.
13을 넣는다면?
double notation이랑 single notation의 처치 방법이 다르다.
LLRRLRRL
경로 지그재그 / 직진인지에 따라서 subtree가 달라질 수 있다. balance가 유지된다.
B-Trees
motivation for B-Trees
index structures for large datasets cannot be sotred in main memory
storing it on disk requires different approach to efficiency
assuming that a disk spins at 7200 RPM, one revolution occurs in 1/120 of a second, or 8.3 ms
crudely speaking, one disk access takes the same times as 200000 instructions
디스크 엑세스하는 것이 느리다.
Motivation (count.)
assume that we use an AVL tree to store about 20 milion records
we end up with a very deep binary tree with lots of different disk access
log2 20000000 is about 24, 0.2 seconds
we know we can't improve on the logn lower bound on search for binary tree
the solution is to use more branches and thus reduce the height of the tree
B-TREE의 아이디어
=> binary 라는 조건을 버려야 height를 낮출 수 있다.
다원 트리
Comparing Trees
Binary trees
Multi-way trees
B-tree can be M-trees
m-way b-tree m원b트리
def) a b-tree of order m is an m-way search tree that either is empty or satisfies the following properties
: the root node has at least two children or a leaf(terminal node)
: all nodes other than the root node and external nodes(terminal) have at most m and at least ceil(m/2) children
내부 노드는 최대 m개, 최소 ceil(m/2) m/2의 올림 값의 children을 갖는다
: all external nodes(terminal node) are at the same level
: the number of keys is one less than the number of children for non-leaf nodes, and at most m-1 and at least ceil(m/2)-1 for leaf nodes => 이 조건은 뭐지?
| m=3 삼원 트리 2-3 tree, min children = ceil(3/2) = 2 degree(internal, children number) = 2, 3 degree(root) = 0,2,3 # keys in a leaf node = 1,2 |
| m=4 (2-3-4 tree) min children = 2 degree = 2,3,4 degree (root) = 0,2,3,4 # keys in a leaf node = 1,2,3 |
| m = 5, min children = 3 |

example : 5원 B-Tree : 2~5개까지 children을 가질 수 있다.
root는 0/2~4개 값을 가질 수 있다.
결국은 순서에 따라 구분되는 ST
* A G F B K D H M J E S I R X C L N T U P
root 단계 :
A B F G
* A G F B K D H M J E S I R X C L N T U P
height 2 단계 :
F
A B / G K
* A G F B K D H M J E S I R X C L N T U P
height 2 단계 :
F
A B D / G H J K
* A G F B K D H M J E S I R X C L N T U P
height 2 단계 :
F J
A B D / G H / K M
* A G F B K D H M J E S I R X C L N T U P
height 2 단계 :
F J
A B D E / G H I / K M R S X
* A G F B K D H M J E S I R X C L N T U P
height 2 단계 :
F J R
A B D E / G H I / K M / S X
A B D E / G H I / K M R S X
* A G F B K D H M J E S I R X C L N T U P
height 2 단계 :
C F J R
A B / D E / G H I / K M / S X
* A G F B K D H M J E S I R X C L N T U P
height 3 단계 :
delete example
J
C F / M R
A B / D E /
* E를 제거한 뒤에, underflow가 아닌지 확인한다.
min children 값보다 작은 value가 있는 경우
=> borrow from a neighbor 왼쪽이나 오른쪽에서 가져온다.
right의 min이 올라간다.
부모를 데러오고 오른쪽 min value가 올라온다.
ㅇㅎㅇㅎ
=> borror할 수 없으면, combine해준다
윗층에서도 다시 combine해준다
K가 underflow가 나면, 다른 곳에서 가져와준다.
delete R
이 구조는 결국 search tree
5원일 때는 2,3,4를 유지해주어야 한다.
overflow => split
underflow => combine
Analysis of B-Trees
the maximum number of items in a B-Tree of order m and height h
height 0(root) m-1
height 1 m(m-1)
height 2 m^2(m-1)
..
height h-1 m^h-1(m-1)
height h m^h(m-1)
sum : m^h+1-1
음청 넓구나
'Computer Science > 자료구조' 카테고리의 다른 글
| 자료구조 | Graph | 숙명여대 학점교류 (0) | 2022.01.07 |
|---|---|
| 자료구조 | Graphs | 숙명여대 학점교류 (0) | 2022.01.06 |
| 자료구조 | Sorting - 2강 | 숙명여대 학점교류 (0) | 2022.01.05 |
| 자료구조 | 이진 트리 구현 (python) | Trees (0) | 2022.01.04 |
| 자료구조 | 정렬 Sorting | 숙명여대 학점교류 (0) | 2022.01.04 |