학점교류로 듣는 숙명여대 자료구조
day 9. 2022.1.3. 월요일
1. Introduction
2. Binary Trees
3. Threaded Binary Trees
4. Heaps
Tree
def) A hierarchical data structure that consists of one or more nodes
계층적 자료 구조
root / sub trees

트리는 그래프의 부분 집합
다 그래프인데, 루트가 독립되어있어서..
노드들이 연결된 것을 그래프라고 한다.
Huffman Coding Tree
Text compression method based on the frequency
example : "time and tide wait for no man"

단말 노드를 만들어준다. 자식 노드를 합해서 부모 노드를 만들어준다.
합이 같아지는 순서가 노드를 만드는 기준이다. (기존의 합보다 같은 순으로)
유일한 트리가 아니고, 여러 가지가 나올 수 있다.

부호를 부여한다면?
스페이스는 11이 된다. 아~ 왼쪽이 0, 오른쪽이 1로 두어서 하게 된다.
빈도 수가 높은 문자는 bit 길이가 짧다
빈도 수가 낮은 문자는 bit 길이가 상대적으로 길다.
출현 빈도와 bit 길이를 반비례하도록 설정하였음. == 가변길이 부호화
10101010110 not
0110011100100011 time
우리의 과제는 허프만 코딩 트리를 정렬해서 만들라는 것
step 1. 부모 노드를 만들어준다. (합이 증가하는 순서대로)
step 2. 부호를 부여해나간다.
w와 f의 부호를 거꾸로 저장되어나간다.
나머지 부호가 저장되어야 한다.
결국 루트에 모든 허프만 코드 트리가 출력되어야 한다.
주의사항 ) 문제에서 제시한 방법이 아니면 불허
용어
노드 : a unit of tree which consists of data and link fields
Degree of node 차수(노드) : number of children of a node
Degree of tree 차수(트리) : maximum of degrees of all nodes
leaf / terminal node : a node whose degree is zero or has no child
level 레벨 : increases by 1 from the root(0) to leaf
height / depth of tree : aximum number of levels, # edges in the longest path
-> 과제에서도 구현해야 하는 것 : node height / node depth / tree height / tree depth 각각 구현
parent & child nodes : level difference is 1 between them
siblings : nodes that have the same parents
ancestors : all upper nodes in path between a node and the root
descendants : all nodes in sub-trees of a node
path : a sequence of nodes and edges connecting a node with a descendant
Internal and External nodes
Internal node (inner node) : a node with at least one child
External node (leaf node) : a node with no children == terminal node
Height and Depth
node height node depth의 계산법
depth : root -> node에서 path 의 수 (number of edges)
height : 는 단말 노드에서 출발해서 계산한다.
tree의 경우, 가장 긴 것, 큰 것을 기준으로 한다.
좀더 정확히 찾아볼 것~! (재귀함수 작성)

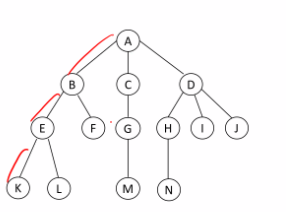
Exercise
siblings of B : C D
Ancestors of K : A B E
Descendant of B : E F K L
Degree of Tree : 3
Degrees of Nodes : F (0) G (1) D (2)
Level of N : 3
Tree height / Depth : maximum level 3
Inner nodes : A B C D E G H
external nodes : K L M N I J K
Representation
- Linear list
sub-trees are represented within round brackets
nested 형태
(A(B(E(K,L),F),C(G(M)),D(H(N),(I,J)))
- Linked list
each tree node consists of one data field and multiple link fields as many as children
몇 개의 자식을 가질 것인지 제한하지 않는 경우 => Generic tree 일반 트리
Generic tree보다 binary tree를 한다.
Binary Trees
* Binary Tree vs generic tree
binary tree는 empty tree를 허용한다.
binary tree는 child order에 sensitive하다
binary tree로 제한하면, 문제를 풀기 쉬워진다.
* max number of nodes at level i
2^i (where i >= 0)
level 0 has (1) node
level 2 has (4) nodes
* max number of nodes in a tree of height h
AT MOST!!
2^h+1 - 1 (where h>= 0) => full binary tree
1 + 2 ^1 + 2^2 + ... + 2^h = a(r^n-1) / (r-1)
=> 외워주어야 한다.
Full binary tree
포화이진트리 (가득가득 찬 경우)
except leaf nodes, the degree of other nodes is all two
a full binary tree of height h has 2^h+1 - 1 nodes
full binary trees satisfy the following
n0 = n2 + 1
n0 = number of leaf nodes
n2 = number of nodes of degree 2
포화
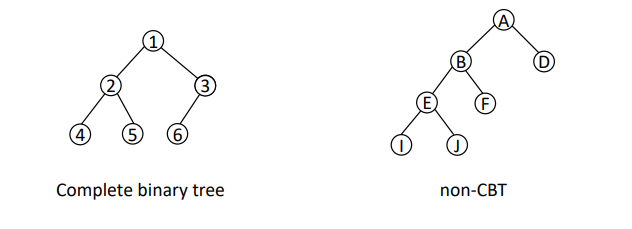
Complete Binary Trees 완전 이진 트리
nodes exist sequentially in left-right, and root-leaf without any missing node in the middle
왼쪽부터 채우는 트리
FBT => CBT, CBT=/=> FBT Complete Binary Tree는 Full Binary Tree의 필요조건
중간에 노드가 비어있는 구조면 안된다.
height (FBT) = O(log2n)
Height (FBT)
prove that height(FBT) = O(log2n) where n is # of tree nodes
1 + 2^1 + 2^2 + 2^3 + ... + 2^h = n ... (1) h >= 0
1 + 2^1 + 2^2 + 2^3 + ... + 2^h + 1 = 2^h+1 ... (2) as n0 = n2 + 1
2^h+1 = n+1
log2(2^h+1) = log2(n+1)
h = log2(n+1) - 1
h = O(log2n)
Height (CBT) = O(log2n) => 숙제
Representation
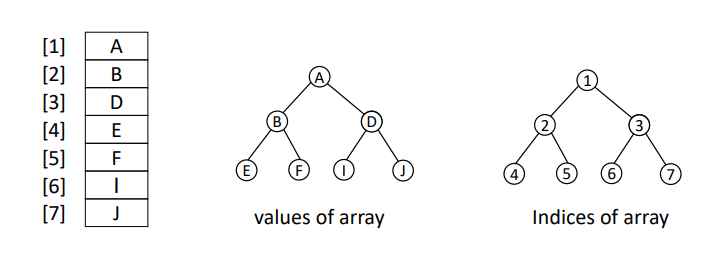
Array Representation
- nodes are stored from array[1] for the following relations
assuming that node(i) is stored at B[i]
- parent of (i) exists at B[i//2], where i > 1 as the root has no parent
- left and right children of (i) exist at B[2i] and B[2i + 1]
- where 2i <= n and 2i+1 <= n as n is # of nodes
Best case : Balanced complete binary tree
wort case : skewed tree with k nodes and height k-1
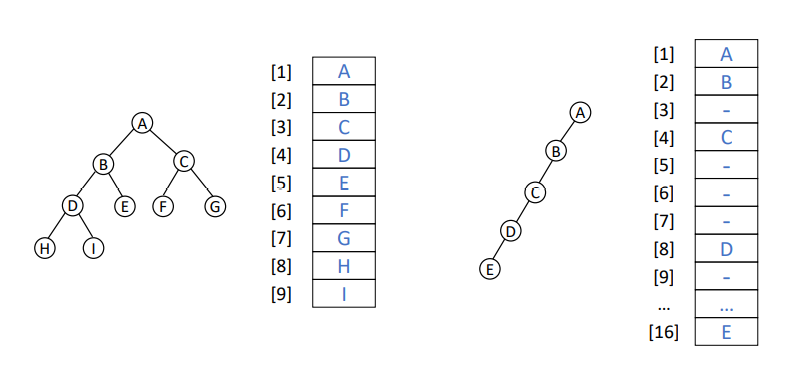
트리의 모양에 영향을 받는다.
Representation
Linked Representation => DLL으로 binary tree 구현
* not affected by tree shape
* no wasted memory space
* efficient to insert/delete nodes
node fields
Linked Representation
* tree is a tree pointer
* all leaf nodes have null links
Tree Traversal
트리는 계층적이고 선형적이지 않기 때문에
탐색 방식이 다양하다.
LVR Inorder 방식은 infix, L = LS, R = RS
LPV postorder 방식은 postfix 방식
preorder VLR 방식은 prefix 방식이다.
Binary trees
expr = A * B + C - D / E
Traversal methods
- postorder
- inorder
- preorder
- level order
postorder
def postorder(tree):
if tree:
postorder(tree.left)
postorder(tree.right)
print("%d" % tree.data)output : A B * C + D E / -
값을 어떻게 계산하는가? postorder가 불린 경우, leftchild
트리가 None이면, 그냥 끝난다.
그 다음에는, 트리가 *일 때 어려움..
C도 부르고.. C가 출력되고..
다 끝났으면, 첫번째 호출로 돌아가서 - 출력
infix
def inorder(tree):
if tree:
inorder(tree.left)
print("%d" % tree.data)
inorder(tree.right)output : A * B + C - D / E
Preorder
def preorder(tree):
if tree:
print("%d" % tree.data)
preorder(tree.left)
preorder(tree.right)Exercises
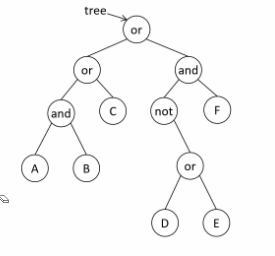
inorder : A and B or C or not D or E and F
postorder : A B and C or D E or not F and or
preorder : or or and A B C and not or D E F
inorder call / tree ptr / action
n = 9, 9 + 5 * 2 = 19
Iterative Inorder
implement inorder traversal method using iterative loop
algorithm
- push nodes into stack with following left-link
- if left node is null, pop a node from stack and print it
- if stack is empty, exit the program
- otherwise, move to the right child of current node, and repeat the above procedure from (1)
time complexity
O(n)
def iterative_inorder(tree):
node = tree
while True:
while node:
push(node)
node = node.left
node = pop()
if not node: break
print("%d" %node.data)
node = node.rightright가서 push하면 나온다.
C를 다시 pop하고, 빼기 까지 나온다.
C, B, A * B + C - right로 가서.. left가 있으므로 / D가 스택에 들어간다.
Level order
visit nodes level by level
=> -+/*CDEAB
implemented by Queue
Algorithm
- add the root into Q initially
- delete a node from Q and print it
- add the children of the node into Q
- repeat the above from step 2 until queue is empty
def levelorder(self, node):
if not node: return
self.add(node)
while True:
node = self.delete()
if node:
print(node.data, end=' ')
if node.left:
self.add(node.left)
if node.right:
self.add(node.right)
else: breakcopy tree
return a duplicate of a tree
def copyTree(tree):
if tree:
temp = None(tree.data)
temp.left = copyTree(tree.left)
temp.right = copyTree(tree.right)
return temp
return NoneEvalutation Tree 수식 평가 트리
a logical expression with boolean variables
- (x1 ^ ~x2) V (~x1^x3) V ~x3
representation
- data : boolean variable (T, F) or logical operators (Not, And, Or)
- value : evaluation result of an expression made by node and its sub-trees
class Node:
def __init__(self, data):
self.data = data
self.value = None
self.left = None
self.right = None
def eval_tree(self, node):
if node:
self.eval_Tree(node.left)
self.eval_tree(node.right)
if node.data == '+':
node.value = node.left.value + node.right.value
elif node.data == '-':
node.value = node.left.value-node.right.value
elif node.data == '*':
node.value = node.left.value * node.right.value
elif node.data == '/':
node.value = node.left.value/node.right.value
else:
node.value = int(node.data)
eval_tree(node)
print(node.value, end=' ')
'Computer Science > 자료구조' 카테고리의 다른 글
| 자료구조 | Binary Trees - 2강 | 숙명여대 학점교류 (0) | 2022.01.04 |
|---|---|
| 자료구조 | Binary Trees | Trees (0) | 2022.01.04 |
| 숙명여대 자료구조 중간고사 족보 | 숙명여대 학점교류 (1) | 2022.01.02 |
| 자료구조 | Hashing Search (0) | 2021.12.31 |
| 자료구조 | doubly linked list | Linked List (0) | 2021.12.31 |