숙명여대 학점교류로 듣는 자료구조
day 10. 2022.1.4. 화요일
Threaded Binary Tree
Heap
Priority Queue
Heap Sort
threaded Binary Tree
스레드 이진 트리
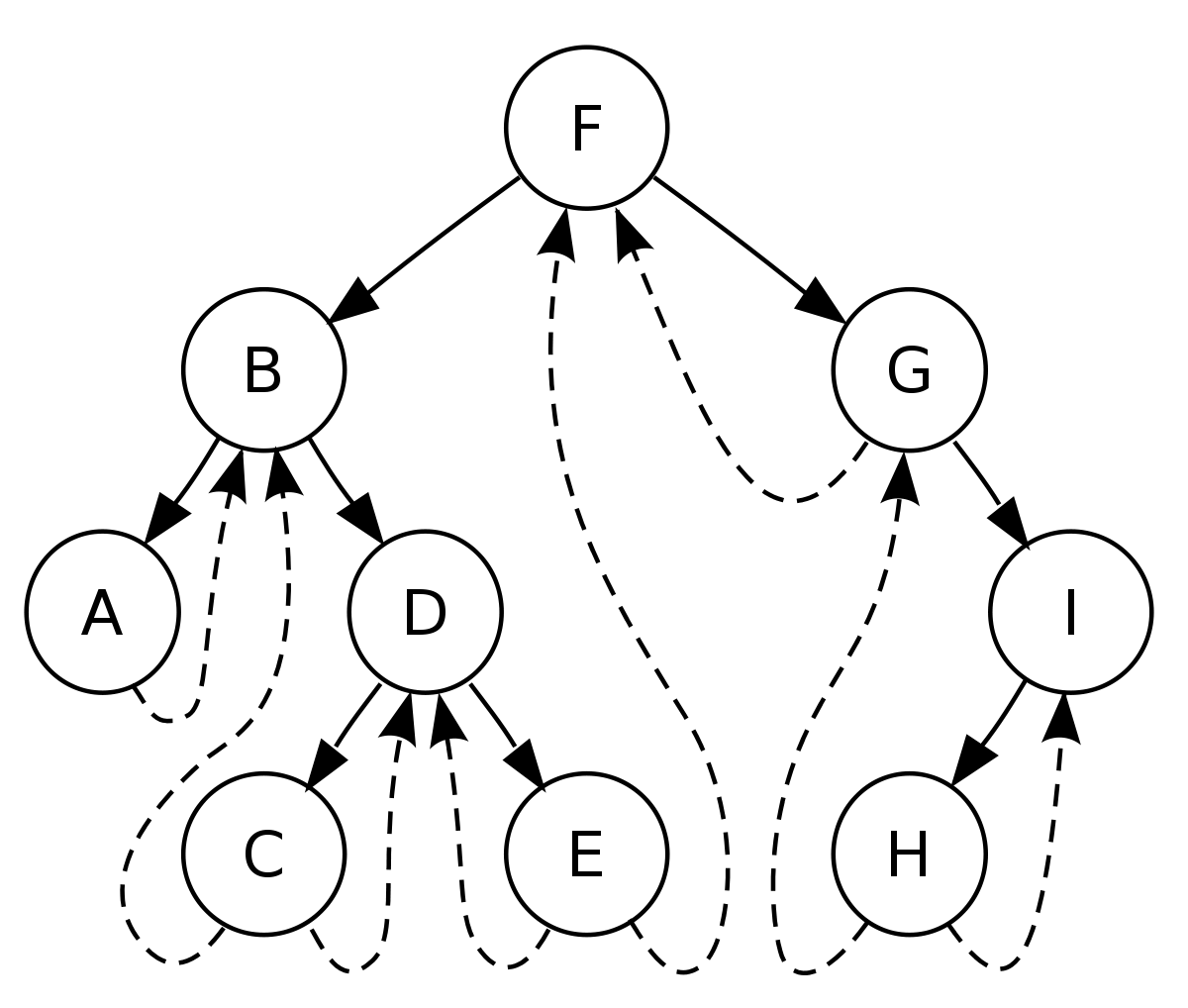
기존 이진 트리를 변경한 것이다.
Binary trees have n nodes and n+1 null links (out of 2n)
null 링크가 참 많다.
null links can be utilized as thread pointers which are used for traversing a tree
thread pointer라는 개념을 트리 탐색에 활용해보자 :)
a thread is a link to the previous or the next node inorder traversal sequence
null link를 thread로 변형해서, 현재 노드의 직전 노드와 다음 노드를 가리키도록 하자는 것이다.
how to create a thread pointer
- a left null link indicated the previous node in inorder sequence
- a right null link indicates the successor node
null link가 두 개가 있다(left, right)
left는 previous node에, right는 다음 노드에 할당한다.
Threaded field
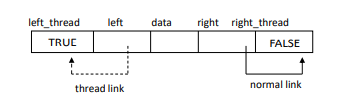
null link인 경우,
left_thread, right_thread field를 추가해준다.
Thread field가 True인 경우 thread link, False인 경우 normal link로 한다.
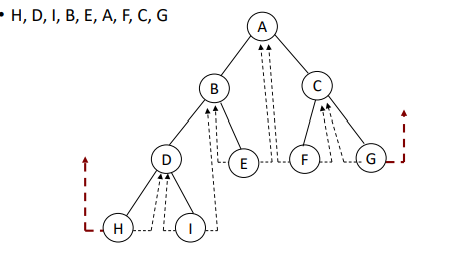
Left는 previous, Right는 다음 링크
* 점선 : thread pointer / link
* 실선 : normal link
Thread link를 쓰면 무엇이 좋은가?
기존에는, 탐색하다 None이 나오면 다음으로 갔다.
Thread link를 쓰면, None이 없어지고 노드를 구분할 필요가 없다.
노말 링크랑 스레드 링크인지를 구분해주어야 한다.
자신의 노드 값을 구분하기 위한 것이다. 단말 링크는 thread 값이 모두 True일 것이다.
단말 노드에 thread field는 전부 True일 것이다.
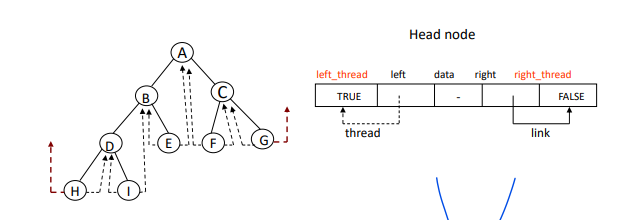
head node : to prevent dangling threads, H and G indicate the head
left_thread, right_thread fields
head node는? left_thread도 자기 자신을, right_thread도 자기 자신을 가리키도록 설정해둔다.
(탐색을 쉽게 하기 위한 장치)
링크 노드가 어딘가를 가리킬 수 있도록 설정해둔 것이다.
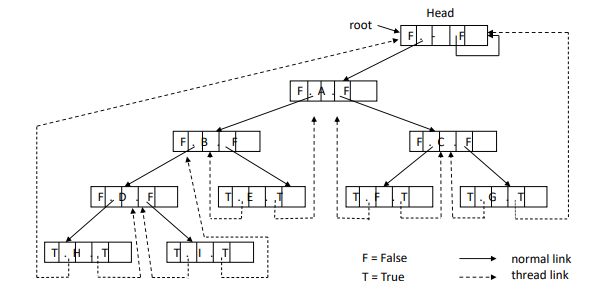
점선은 전부 thread
- 활용 방향 ) by following right link from the root, it is possible to traverse the tree by inorder
case 1. right link == normal
terminal node를 발견할 때까지, 이 노드에 연결된 left node까지 찾아서 내려간다.
해당 terminal node (H)가 첫번째 방문 노드가 된다.
case 2. right link == thread
다음 방문 노드 따라간다. (D)
결론 : H > D > I > B > E > A > F > G > C
- 단말 노드의 link는 thread, 내부 노드의 link는 normal link로 되어있다.
- right 링크만 따라가주면 된다는 결론 :D
구현
Implementation (iterative)
- iterative implementation
tbt_inorder() => main function
successor() => find a successor node
time complexity O(n)
def tbt_inorder(tree):
temp = tree
# tree가 잘 달려있다면, ...
while True:
temp = successor(temp)
if temp == tree: break
print("%3c" % temp.data)
def successor(tree):
temp = tree.right
# if normal link
if not tree.right_thread:
# find a left leaf node
while not temp.left_thread:
temp = temp.left
# left thread를 반환해준다
return tmp
- 노드 추가 : thread field update
- 노드 삭제
등 해보기 :D
Heap
max heap
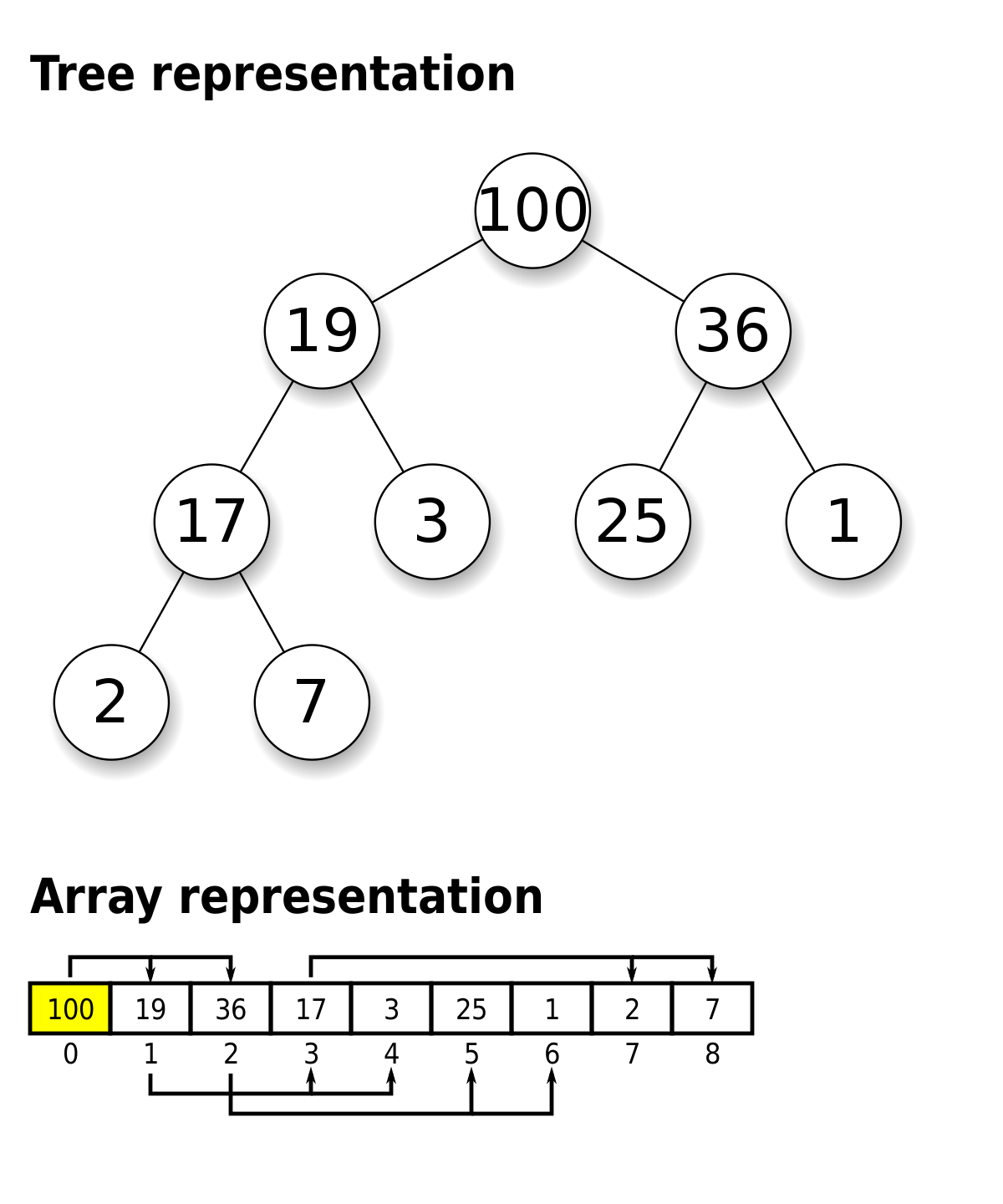
최대 트리 max tree
: a tree that each node is greater than those of its children in value
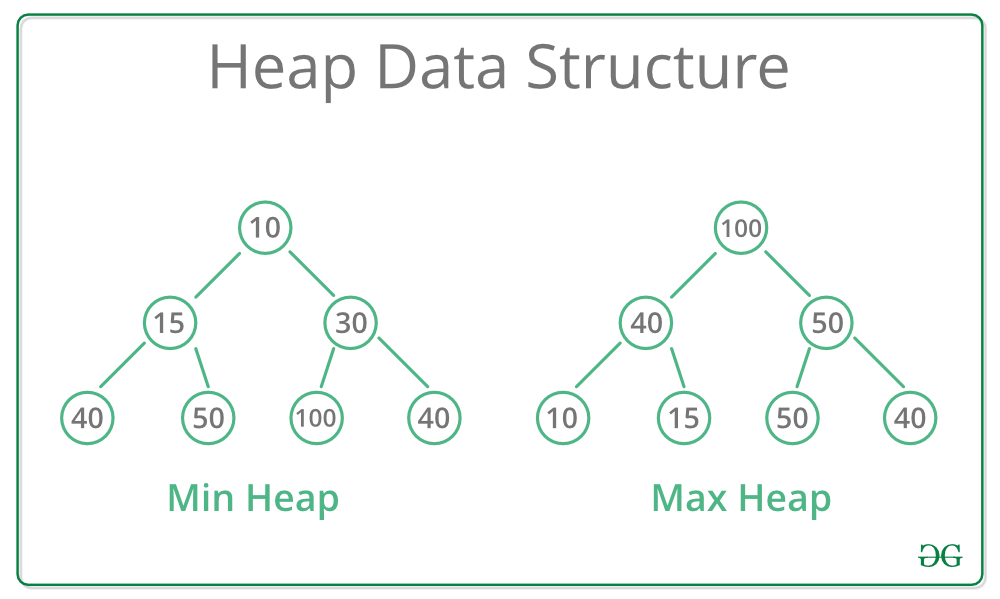
Max heap
: a max tree that satisfies the properties of complete binary tree (좌->우, 상->하로 채워진 트리)
: CBT - Nodes must be present in left-right and root-leaf order with no missing node
: root - the node who has the max key in tree
=> 최댓값을 찾기에 유용하다
=> 우선순위 등
min heap
* min tree - a tree that each node is smaller than its children in key value
* min heap
- a min tree that satisfies the property of complete binary tree
- root : the smallest key in tree
- ex) applications that find the min value in tree
- ex) min heaps
=> 최솟값 탐색에 유용하다.
heap
대충 어떤 앤지는 알겠으니, 노드 추가 / 삭제 / 정렬 에 대해 알아보자!
1. node insertion algorithm
a new node is added after the last node
to satisfy max heap properties(CBT and Max tree)
a new node is repeatedly compared with its parent up to the root to find the right position
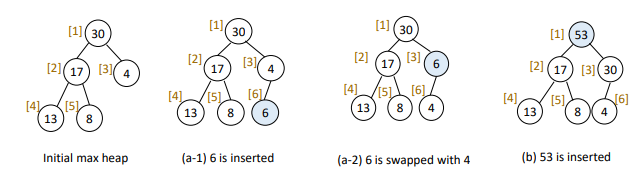
일단 말단 노드에 삽입한 뒤에 부모 노드와 비교해가면서 올려준다 :)
* 여기서 [1], [2]는 배열의 index를 의미한다. 0에는 저장해주지 않는다. 그 이유는 앞선 tree 포스팅 참고~!
Insertion and Deletion in Heaps - GeeksforGeeks
파이썬으로 heap을 구현해보자
because heap is CBT, array is better than the linked list
class Heap:
def __init__(self, size):
self.size = size
self.heap = [None]*size
self.count = 0
def isEmpty(self):
# element가 1개 들어가는 것이 empty
# [0]에는 None이 들어가기 때문이다.
return self.count == 1 # 0 is dummy
def isFull(self):
return self.size - 1 == self.count
def add_heap(self, item):
if self.isFull(): return
self.count += 1
i = self.count
# i가 첫 노드가 아니며,
# item이 i의 부모보다 클 때
while i != 1 and item > self.heap[i//2]:
self.heap[i] = self.head[i//2] # 부모랑 자식의 자리를 바꿔준다
i //= 2 # 위에 거랑 다시 비교해준다
self.heap[i] = item
print("%2d" %item, end='')
print(self.heap)
time complexity
O(log2n) (n = tree height)
2. node delete algorithm
the root (max) is deleted from heap
heap rebuilding => O(log2n)
algorithm
- the root is saved and the position is replaced with the last node
- if R is greater than its child, rebuilding is completed
- if any child is greater than R, it is swapped with R
- repeat this comparison with the next lower level nodes to leaf until finding a right position
def del_heap(self):
if self.count == 0:
print("empty heap")
return
item = self.heap[1]
temp = self.hea[self.count]
self.heap[self.count] = None
self.count -= 1
parent = 1
child = 2
while child <= self.count:
if child < self.count and \
self.heap[child] < self.heap[child+1]:
child += 1
if temp >= self.heap[child]: break
self.heap[parent] = self.heap[child]
parent = child
child *= 2
if self.count != 0:
self.heap[parent] = temp
return item
3. heap sort
algorithm
- create a binary tree with n items
- rebuild a max heap by makeheap() with unsorted items
- swap the root with the last item for saving the largest item
- except for sorted items, repeat the above procedures from step 2
4. max heap
step 0. initial entries를 배열에 저장한다.
initial entries : 24, 7, 80, 3, 64, 15, 50, 10, 42, 18
step 1. makeheap()
한꺼번에 다 넣고, heap으로 순서를 바꾸어준다.
starting from node i (i=n//2), if a bigger child(2i, 2i+1) is greater than its parent i, then swap them
repeat the above procedures with decreasing i up to the root
step 2. rebuild heap()
for i in range(n//2, 0, -1):
makeheap(num, i, n)순서대로 각각 5번 makeheap()을 해준다.
example
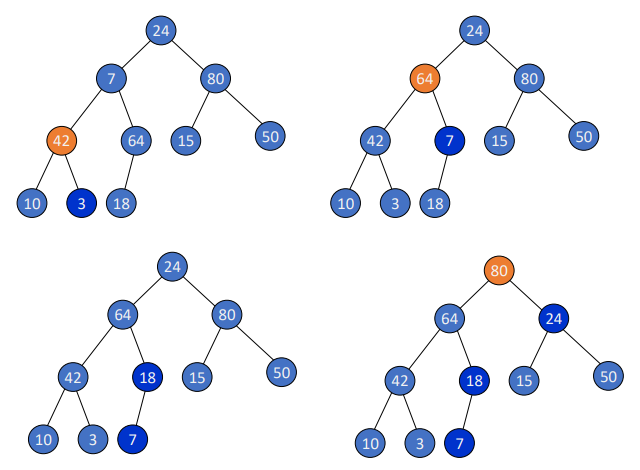
final code
def sort(self):
n = self.size - 1
for i in range(n//2, 0, -1):
self.makeheap(i, n) # 초기 최대 힙
print(self.num)
for i in range(n-1, 0, -1):
self.swap(1, i+1) # max 값을 마지막 원소와 교환
self.makeheap(1, i) # 재정렬할 노드, 노드 수
print(self.num)
def makeheap(self, root, n):
# 재정렬할 root, node 수
temp = self.num[root]
child = 2 * root # 왼쪽 자식 노드
while child <= n:
if child < n and self.num[child] < self.num[child+1]:
child += 1
if temp > self.num[child]: break
# 부모와 자식 노드 중 큰 것과 비교
else:
# 자식 노드를 부모 위치로 이동
self.num[child//2] = self.num[child]
# 한 레벨 낮춘다
child *= 2
self.num[child//2] = temp다시 직접 구현해보기 :)
time complexity : O(nlog2n)
Priority Queue
queue : waiting line (buffer)에 주로 사용된다.
priority queue
* queue items are sorted by the priority
* an item with the highest priority is deleted first from queue
* max heap is suitable for implementing such priority queue
ex) os job scheduler
* admin's job => highest priority
* user's job => low priority
min heap is good for scheduling shortest job first scheme
elements are deleted by priority (7 > 6 > 5 > 4)
implementation의 방식에 2 가지가 있다.
<unordered>
unordered 방식은 들어갈 때는 정렬하지 않고, delete할 때 우선순위를 중심으로 처리하는 것이다.
insert = O(1), delete = O(n)
unordered array
unordered linked list
<ordered>
들어갈 때 우선순위에 맞추어 처리하는 것이다.
insert = O(n), delete = O(1)
ordered array
ordered linked listd
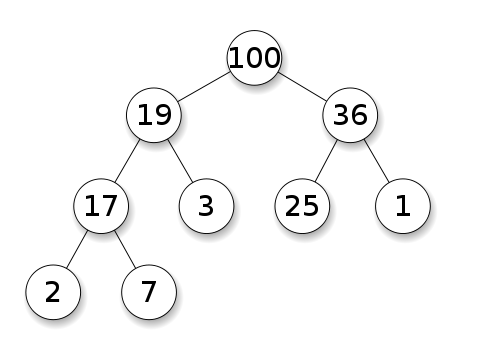
heap needs rebuilding whenever inserting/deleting a node
heap rebuilding time is proportional to tree height
=> 트리의 높이가 비교 횟수가 된다. 결국 log2n 만큼 걸림 => 훨씬 효율적!
insert = O(log2n), delete = O(log2n)
'Computer Science > 자료구조' 카테고리의 다른 글
| 자료구조 | 이진 트리 구현 (python) | Trees (0) | 2022.01.04 |
|---|---|
| 자료구조 | 정렬 Sorting | 숙명여대 학점교류 (0) | 2022.01.04 |
| 자료구조 | Binary Trees | Trees (0) | 2022.01.04 |
| 자료구조 | Trees | 숙명여대 학점교류 (0) | 2022.01.03 |
| 숙명여대 자료구조 중간고사 족보 | 숙명여대 학점교류 (1) | 2022.01.02 |