Trees
Introduction
Binary Trees
Threaded Binary Trees
Heaps
Introduction

트리
트리는 루트, 서브 트리로 구성된 계층형 자료구조다.
트리는 하나 이상의 노드가 있어야 하며,
서브 트리는 부모 노드를 제거한 뒤 남아있는 부분 트리를 말한다.
트리는 계통도, 조직도, 폴더 등 계층적으로 자료를 관리하는 분야에 활용된다.
트리의 종류 : rooted tree, non-rooted tree (graph)
예시 - 허프만 코딩 트리

허프만 코딩 트리는 "time and tide wait for no man"과 같은 텍스트를 빈도에 기반해서 압축하는 트리이다. 출현 빈도가 높은 글자는 짧은 비트로, 낮은 빈도는 상대적으로 긴 비트로 할당한다. 이를 통해 효율적으로 글자를 표현하고자 하는 것이다. time and tide waits for no man의 문자열을 빈도에 따라 정렬하면, 다음 사진과 같이 된다.
허프만 코딩 트리는 상향식으로 만드는 Binary Tree로, Full Binary Tree로 구현하는 것이다. 이때 Full Binary Tree는 노드가 자식을 0개 혹은 2개씩 갖는 트리 형태를 말한다.

허프만 코딩 트리에서는 빈도에 따라 정렬된 것을 트리로 표현해낸다.
허프만 코딩 트리를 만드는 방법은 다음과 같다.
1. 각 문자로 개별적인 노드를 만든다. (빈도 수 표기)
2. 빈도수가 작은 두 트리를 합쳐서 큰 트리(부모 노드, 부모 노드의 빈도 수는 자식 노드 빈도 수의 합)를 생성하는 과정을 반복한다.
3. 이때 왼쪽은 0, 오른쪽은 1로 표기한다.

파이썬 구현은 추후에
데이터 구조 - 허프만 트리 (파이썬 구현) - 코드 세계 (codetd.com)
를 참고해보려고 한다.
용어들
- Node : data / link를 가진 트리의 단위
- Degree of node : 노드의 차수, 특정 노드에 연결된 서브 트리의 수
- Degree of tree : 트리의 차수. 모든 노드의 차수 중 최댓값
- Leaf / terminal node : 단말 노드. 자식 노드가 없는 노드.
- level : 루트 레벨에서 단말 노드 방향으로 1씩 증가하여 표현한다 ( 부모 - 자식 = 1)
- height / depth of tree : 레벨의 최댓값
- parent & children nodes : 노드 레벨 차이가 1인 관계
- siblings : 같은 부모 노드를 공유하는 노드들
- Ancestors : 해당 노드위에 있는 모든 노드와 루트
- Descendants : 특정 노드의 서브 트리에 있는 모든 노드
- path : 특정 노드에서 어딘가로 잇는 노드와 edge(선분)들
Internal and External nodes
internal node (inner node) : 자식이 최소한 1개 이상인 노드
external node (leaf node) : 자식이 없는 단말 노드
예제

1. node의 height, depth
A : height = 3, depth = 0
B : height = 2, depth = 1
E : height = 1, depth = 2
K : height = 0, depth = 3
2. Siblings of B : C, D
3. Ancestors of K : E B A
4. Descendants of B : E F K L
5. Degree of Tree : 3
6. Degrees of Nodes
F : 0
G : 1
D : 2
7. level of N : 3
8. Tree height / Depth : 3
9. Inner nodes : 10 제외 모두
10. External nodes : K L F M N I J
Representation
트리 구조는 linear list 혹은 linked list 형태로 구현된다.
- Linear list
괄호를 이용하여 계층적인 서브 트리를 표현한다.
예를 들면, (A(B(E(K L)F)C(G(M))D(H(N)I J)))
- Linked list
각 트리 노드는 데이터 필드와 링크 필드를 가진다. 제한하지 않는 경우, 아주 많은 자식 노드를 가질 수 있다.
이진 트리 Binary Trees
이진 트리는 자식 노드의 최대 수가 2인 트리이다.
이진 트리의 차수는 2이고,
일반 트리와 다른 점 두 가지는 [1] 빈 트리를 허용한다 [2] 자식 노드의 좌우를 구별해준다는 것이 있다.
이진 트리에서 레벨 i에 존재할 수 있는 최대 노드 수는 2^(i-1)개이다.
예를 들면, 루트(레벨 1)에서의 최대 노드 수는 1개, 레벨 3에서 최대 노드 수는 4이다.
높이가 h인 이진 트리의 최대 노드 수는 2^h+1 - 1이다.
Full binary tree 포화 이진 트리
단말 노드를 제외하고, 모든 노드의 차수 Degree가 2인 트리를 말한다.
(이때 차수란 특정 노드에 연결된 서브 트리의 수를 말한다)
FBT Full Binary Tree는 Height가 O(log2n)이다.
| <증명> FBT는 각 레벨의 최대 노드만큼 채워져있으므로, 각 이진 트리 높이에서는 노드 수가 2^(h-1)이다. h가 이진 트리의 높이 (h >= 0), n이 이진 트리의 전체 노드 수일 때, 1 + 2^1 + ... + 2^h = n n0 = n2 + 1이므로 1 + 2^1 + ... + 2^h + 1 = 2^(h+1) 1 + 2^1 + ... + 2^h = 2^h+1 - 1 식을 계산해주면, 2^(h+1) - 1 = n 2^(h+1) = n + 1 로그를 씌워주면, log2(2^h+1) = log2(n+1) h = log2(n+1) - 1 n이 크다고 가정하고, 점근적 표기법으로 바꾸면, h = O(log2n) |
Complete binary trees 완전 이진 트리

Complete Binary Tree는 노드가 루트부터 leaf node 방향으로, 왼쪽에서 오른쪽 방향으로 빈 노드 없이 순서대로 모든 노드가 존재하는 이진 트리이다.
Full Binary Tree는 CBT의 충분 조건이고, CBT는 FBT의 필요조건이다.
이진 트리의 표현
이진 트리를 배열, 연결 리스트를 사용해서 표현할 수 있다.
이진 트리의 배열 표현
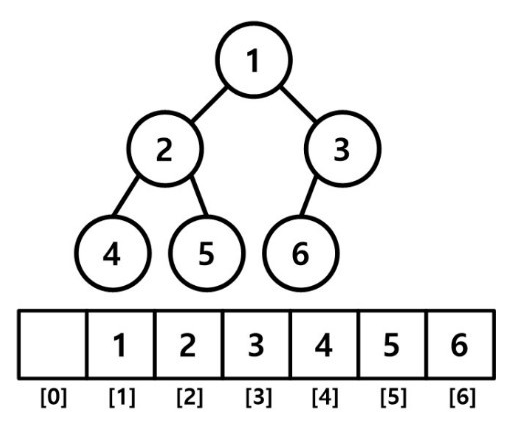
이진 트리의 노드를 순서대로 저장한다.
저장하는 순서는 루트 -> 단말 노드 방향, 좌에서 우 방향이며 배열의 1번부터 저장한다.
A[i]의 부모 노드는 A[i/2]에,
A[i]의 자식 노드는 A[2i]와 A[2i+1] 노드에 저장된다.
배열 0번부터 저장할 경우, 2i를 이용한 계층적 저장법을 활용할 수 없으므로 배열 1번부터 저장한다.
Full Binary Tree의 저장 효율이 가장 좋으며, Skewed Tree는 효율이 좋지 못하다.
이진 트리의 연결 리스트 표현
연결 리스트에 표현하면, 트리 형태에 상관없이 저장 효율을 유지할 수 있다.
각 노드는 data field, left link, right link로 구성된다.
leaf node는 null link를 갖는다.
class Node:
def __init__(self):
self.data = None
self.left = None
self.right = None
이진 트리 탐색 Tree Traversal
이진 트리의 각 노드를 순서대로 방문하여 데이터 값을 받아오는 것을 트리의 탐색이라고 한다.
Binary search, traversal의 방식에는 크게 3가지, Inorder / postorder / preorder / level order 방식이 있다.
- Inorder LVR
- Postorder LRV
- Preorder VLR
- level order
Inorder LRB
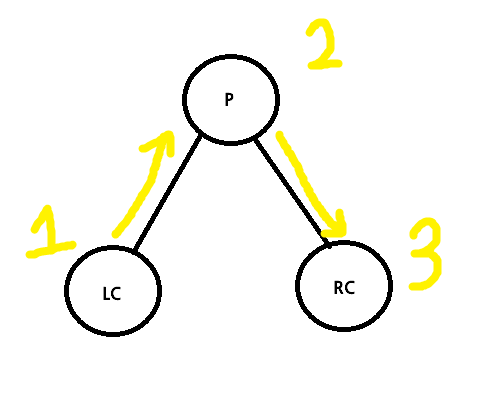
def inorder(tree):
if tree:
inorder(tree.left)
print("%d" % tree.data)
inorder(tree.right)
Postorder LRV
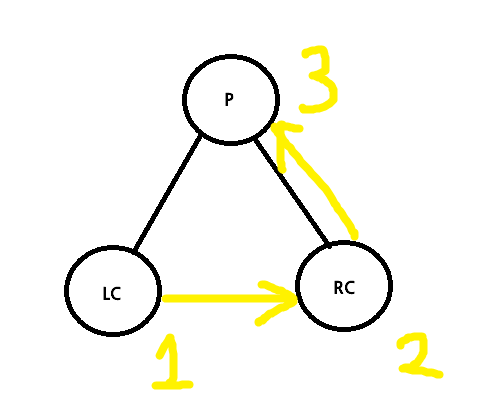
def postorder(tree):
if tree:
postorder(tree.left)
postorder(tree.right)
print("%d" % tree.data)
Preorder VLR
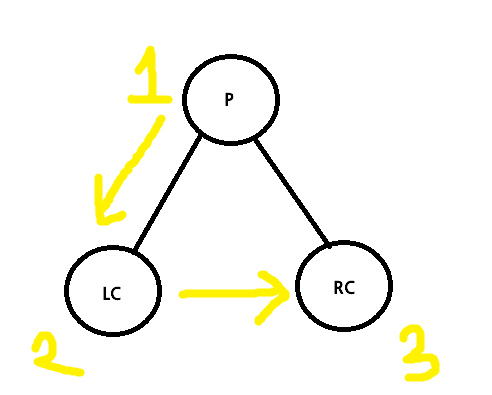
def preorder(tree):
if tree:
print("%d" % tree.data)
preorder(tree.left)
preorder(tree.right)
exercises
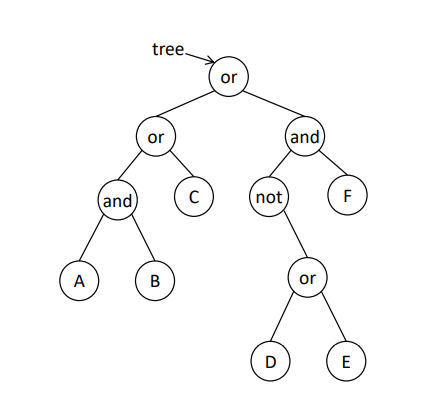
- Inorder
A and B or C or not D or E and F
- postorder
A B and C or D E or not F and or
- preorder
or or and A B C and not or D E F
to be continued.....
iterative inorder
level order
copy tree
evaluation tree
'Computer Science > 자료구조' 카테고리의 다른 글
| 자료구조 | 정렬 Sorting | 숙명여대 학점교류 (0) | 2022.01.04 |
|---|---|
| 자료구조 | Binary Trees - 2강 | 숙명여대 학점교류 (0) | 2022.01.04 |
| 자료구조 | Trees | 숙명여대 학점교류 (0) | 2022.01.03 |
| 숙명여대 자료구조 중간고사 족보 | 숙명여대 학점교류 (1) | 2022.01.02 |
| 자료구조 | Hashing Search (0) | 2021.12.31 |