학점교류로 듣는 숙명여대 자료구조 수업
day 13. 2022.1.7. 금요일
graph representation
adjacency matrix
adjacency list : linked / array
adjacency matrix

n*n matrix, where n=# of vertices
A(i, j) = 1, iff (i,j) is an edge, otherwise 0
self edge = 0
무방향 그래프이기 때문에 대칭으로 그래프가 그려져있음
Diagonal entries are zero
adjacency matrix for undirected graph is symmetric
A(i, j)=A(j, i)
Adjacency Matrix (Digraph)

방향 그래프의 경우
나가는 간선이 진출 간선, 들어오는 간선이 진입 간선이다.
진출 간선(차수), 진입 간선(차수)
들어오는 것, 나가는 것 중 하나를 정해 count 해준다.
진출 간선, 진입 간선
Diagonal entries are all zero
adjacency matrix for diagraphs need not be symmetric
cf) inverse adjacency matrix / list
양방향으로 간선이 없으면, 대칭이 될 수 없다.
진출 간선을 따지기도 한다.
진입 간선만 포함한 리스트 : inverse adjacency matrix / list라고 한다.
adjacency matrix
n^2 bits of space
for an undirected graph, either lower or upper triangle is required excluding diagonal
(n-1)*n/2 bits
O(n) time to find vertex degree and/or vertices adjacent to a given vertex
어떤 정점과 인접한 애가 누군지를 알기 위해 O(n) time이 걸린다.
정점의 인접성(차수)을 계산하는 데 걸리는 시간복잡성은? O(n)
그래프 전체의 인접성을 계산하려면, O(n^2)이 걸린다.
Adjacency Lists
adjacency list for vertex i is a linear list of vertices adjacent from vertex i
an array of n adjacency lists
aList[1] = (2,4)
aList[2] = ...
Linked Adjacency Lists

each adjacency list is a chain
array length = n # 노드 수 만큼의 head가 필요하다
# of chain nodes = 2e (undirected graph) # 간선 수의 2배 edge
# of chain nodes = e (digraph) # 간선 수 만큼 존재
Weighted graphs
* edge weight
* adjacency matrix : c(i, j) = cost of edge (i, j)
* adjacency lists : a node has (adjacent vertex, edge weight)
원래 matrix에 1을 적는데, edge weight을 edge의 cost로 적는다.
3 7 5 등등
Graph Search Methods
DFS, BFS
경로가 있느냐 : a vertex u is reachable from vertex v iff there is a path from v to u
A search method starts at a given vertex v and visits/labels every vertex that is reachable from v
탐색 방법으로 해결한다.
Many graph problems solved using a search method
- a path from one vertex to another
- is the graph connected?
- find a spanning tree(사이클이 없는 연결된 sub tree)
commonly used search methods
- DFS : Depth - First Search
- BFS : Breath - First Search
Depth - First Search
sudo code
def dfs(v):
# v를 방문한 것으로 표시해라
label vertex v as reached
# 인접한 것 중에서 방문하지 않은 것에 대해서
for (each unreached vertex u adjacent from v):
# 탐색하라
dfs(u)
시작 노드에서 인접한 걸 모두 방문하고 나서, 층위를 바꾸어 방문하는 것이 : BFS
DFS는 일단 쭉 내려간 뒤에 진행한다.
algorithm
step 0. 가능한 동안에 임의로 다음 인접한 노드를 골라 재귀호출한다.
step 1. 만약 탐색할 곳이 없으면, backtracking으로 9로 돌아간다.
step 2. 최초 호출 노드로 돌아가면, DFS가 종료된다.
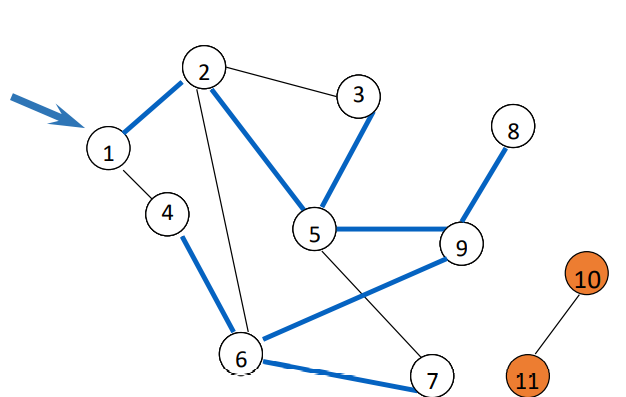
all vertices reachable from the start vertex (including the start vertex) are visited
* path from vertex v to u
start a depth-first search at vertex v
terminte when vertex u is visited or when dfs ends(whichever occurs first)
* time complexity
O(n^2) when adjacency matrix used
O(n+e) when adjacency lists used ( e : # of edges )
구현
class Node:
def __init__(self, value):
self.data = value
class Graph:
def __init__(self):
self.graph= {}
self.visit = []
def create(self, v, data):
node = Node(data)
if v not in self.graph:
self.graph[v] = []
self.graph[v].append(node)
def dfs(self, v):
self.visit.append(v)
for node in self.graph[v]:
if node.data not in self.visit:
self.dfs(node.data)
g = Graph()
# graph 표현 : 1->2, 1->3으로 연결됨
for v, node in [(1,2),(1,3), (2,1), (2,4), (2,5), (2,7), (3,1), (3,4), \
(3,5), (4,2), (4,3), (4,7), (5,2), (5,3), (5,6), (5,8), (6,5), (6,7), (6,8), (7,2), (7,4), (7,6), (8,5), (8,6)]:
g.create(v, node)
g.dfs(1)
print("dfs ", g.visit)* DFS 신장 트리
* 1을 방문해서 반복적으로 방문하고..
if the graph connected?
start a dfs at any vertex of the graph
graph is connected iff all n vertices get visited
time
: O(n^2)
: O(n+e)
connected components
start a depth-first search at any as yet unvisited vertex of the graph
newly visited vertices define a component
repeat until all vertices are visited
spanning tree 신장 트리
: 모든 정점이 연결되었으며, 사이클이 없는 sub tree
를 찾으면 더 효율적이다.
찾는 방법
start a dfs at any vertex of the graph
if graph is connected n-1 edges used to get to unvisited vertices define a spanning tree (DFSpanning tree)
time complexity
Breath-First Search
visit start vertex and put into a FIFO queue
repeatedly remove a vertex from the queue, visit its unvisited adjacent vertices, put newly visited vertices into the queue
similar to level order traversal for trees
=> 재귀호출 말고 queue를 사용한다.
인접한 노드를 하나씩 모두 방문하는 형태로 진행한다.
흥미롭구만
queue가 empty 될때까지 반복
훨씬 직관적이다.
class Graph:
def __init__(self):
self.graph= {}
self.visit = []
self.queue = []
def create(self, v, data):
node = Node(data)
if v not in self.graph:
self.graph[v] = []
self.graph[v].append(node)
def addq(self, v):
self.queue.append(v)
def deleteq(self):
if self.queue: return self.queue.pop(0)
else:
print("Queue Empty")
def bfs(self, v):
self.visit.append(v)
self.addq(v)
while self.queue:
v = self.deleteq()
for node in self.graph[v]:
if node.data not in self.visit:
self.visit.append(node.data)
self.addq(node.data)
g = Graph()
for v, node in [(1,2),(1,3), (2,1), (2,4), (2,5), (2,7), (3,1), (3,4), \
(3,5), (4,2), (4,3), (4,7), (5,2), (5,3), (5,6), (5,8), (6,5), (6,7), (6,8), (7,2), (7,4), (7,6), (8,5), (8,6)]:
g.create(v, node)
g.visit=[]
g.bfs(1)
print("bfs ", g.visit)
time complexity
each visited vertex is put on the queue exactly once
when a vertex is removed from the queue, we examine its adjacent vertices
• Edges used to reach unlabeled vertices define a depth-first spanning tree when the graph is connected
O(n+e)
minimum-cost spanning tree
최소비용 신장 트리
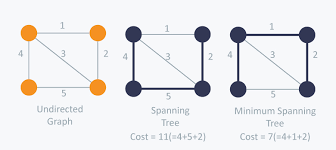
for weighted connected undirected graph
find a spanning tree that has minimum cost
cost of spanning tree is sum of edge costs
edge rejection strategies
cycle을 찾아 high cost를 삭제하는 방법
edge selection strategies
비용이 낮은 것부터 찾아 삭제하는 방법
* kruskal's method
n-vertex 0-edge에서 시작한다.
사이클이 생기면 거절한다.
* prim's method
start with a 1-vertex tree and grow it into an n-vertex tree
정점 하나가 주어지고, 연결된 간선으로 tree를 찾는 방법
* solin's method
kruskal + prim
Kruskal's method
비어있는 forest에서 edge를 하나씩 생성한다.
consider edges in ascending order of cost
edge (1,2) is considered first and added to the forest
총 간선이 n-1개로 줄었다.
신장 트리를 찾았다~!
min-cost spanning tree
method마다 spanning tree의 형태가 다를 수 있다.
prim's method
start with any single vertex tree
정점 한 개만 두고 시작한다.
인접한 정점 중 가장 cost가 저렴한 정점을 갖다둔다.
1 - 2 - 3에 연결된 것 중 가장 저렴한 것은 4
그 다음 저렴한 것 5와 연결된다.
solin's method
step 0. start with a forest that has no edgesstep 1. 각 정점에 연결된 간선 중에, 모든 애들이 다 고른다. 1번은 2, 2번은 2, 3번은 4, 4번은 4, 5번은 6, 6번도 6, 7번도 3, 8번도 3을 고르게 된다. => 2 연결=> 4 연결=> 6 연결 => 3 연결step 2. 연결된 간선을 기준으로 이들을 연결하는 최소 비용을 고른다. 1-2는 7, 3-4는 10, 7-8은 14
pseudocode for kruskal's method
start with an empty set T of edges
while E is not empty and |T| != n-1:
let (u,v) be a least-cost edge in E
E = E - {(u,v)}
if (u,v) does not create a cycle in T:
add edge (u,v) to T
if |T| == n-1:
T is a min-cost spanning tree
else:
network has no spanning tree=> 구현해볼 것
cycle check- find/union
8개의 정점의 집합을 구하고
합집합을 계속해서 만들어내는 것이다.
같은 집합에서는 또 간선이 사용되면 안된다.
다른 집합에 있을 때만 tree head set을 구해야함
'Computer Science > 자료구조' 카테고리의 다른 글
| 자료구조 구현 | selection sort, bubble sort, insertion sort, shell sort, quick sort (python 구현) | 정렬 (0) | 2022.01.08 |
|---|---|
| 자료구조 | Shortest Path and Activity Network | 숙명여대 학점교류 (0) | 2022.01.07 |
| 자료구조 | Graphs | 숙명여대 학점교류 (0) | 2022.01.06 |
| 자료구조 | Binary Search Trees | 숙명여대 학점교류 (0) | 2022.01.06 |
| 자료구조 | Sorting - 2강 | 숙명여대 학점교류 (0) | 2022.01.05 |