학점교류로 듣는 숙명여대 자료구조
day 13. 2022.1.7. 금요일
Shortest Path and Activity Network
shortest path finding
dijkstra algorithm
floyd-warshall algorithm
transitive closure matrix
activity network
shortest path problems
directed weighted graph
path length is sum of edge weights on path
the vertex at which the path begins is the source vertex
the vertex at which the path ends in the destination vertex
single source, single destination
single source, all destinations
all paths
greedy algorithm
- possible algorithm
leave source vertex using cheapest/shortest edge
leave new vertex using cheapest edge subject to the constraint that a new vertex is reached
continue until destination is reached
- greedy algorithm
local optimization => 그 시점에 가장 유리한 선택을 내리는 알고리즘이다. global optimization은 아님.
constructed 1 to 7 path
: path length = 12
: not shortest path. algorithm doesn't work
dijkstra's method
single source all destinations
need to generate up to n (n is number of vertices) paths (including path from source to itself)
Dijstra method
construct these up to n paths in order of increasing length
assume edge costs (lengths ) are >= 0
first shortest path is from the source vertex to itself. the length of the path is 0
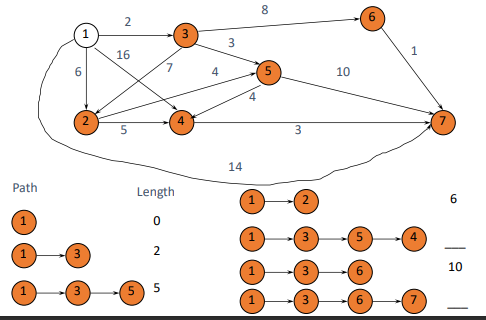
어떤 걸 선택해야 가장 짧은가.
1과 3을 선택해야 한다.
경로가 2가 된다.
간선을 하나만 추가해서 짧은 것을 찾아준다.
3에서 연결해주어도 좋다. 1 3 5를 보면 길이가 5.
간선을 제공했을 때 가장 짧은 것
1,3,5,4가 나오면 9
1,3,6 10
1,3,6,7은 11
마지막에 6-7로 1을 추가해주니 11이 나오게 됨
프로그램으로 돌리면, 알아서 찾아준다..
경로가 증가하는 방향으로 모든 path를 찾아줌
next shortest path is the shortest one edge extension of an already generated shortest path
shortest path from the source 1 to all ther destinations
representation
d, p array가 필요함 distance, previous
- d[i] : source부터 i까지 도달하는 데 까지 걸리는 거리
- p[i] : vertex just before vertex i on the shortest one edge extension to i
1에 연결된 간선은 모두 처리한 것이다.
그 다음에는 가장 짧은 것을 가져온다.
1에서 출발
1-3이 선택되고..
1-3에서 가장 적게 늘어나는 경로는 1-3-5
1-3-5에 연결된 간선을 저장하면? 1-3-5-4로 가면, 더 짧은 경로가 나온다
원래대로 14로 두고, 짧은 거리가 생기면 업데이트해준다
11은 더이상 간선이 없으니 끝나게 된다.
모든 정점으로 가는 짧은 경로를 찾아낸 것이다.
결과물
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| length | |||||||
| prev | |||||||
DS for Dijkstra's Algorithm
Dijkstra's algorithm
implement d[] and p[] as 1D arrays
keep a linear list L of reachable vertices to which shortest path is yet to be generated
select and remove vertex v in L that has smallest d[] value
updata d[] and p[] values of vertices adjacent to v
class Node:
def __init__(self, node, weight):
self.data = node
self.weight = weight
class ShortestPath:
def __init__(self):
self.graph = {}
self.visit = []
self.dist = {}
self.prev = {}
self.min_list = {}
def create(self, v, dest, weight):
node = Node(dest, weight)
if v not in self.graph:
self.graph[v] = []
self.graph[v].append(node)
def pick_min_dist(self):
temp = []
for v, cost in self.min_list.items():
temp.append((cost, v))
temp = sorted(temp)
cost,v = temp.pop(0)
print("Next min cost vertex is", v)
self.min_list.pop(v)
return v
def dijkstra(self, v):
if v not in self.visit:
self.visit.append(v)
else: return
if v not in self.graph:
print("end of search")
return
for node in self.graph[v]:
vertex = node.data
cost = node.weight
if vertex not in self.dist or cost+self.dist[v]<self.dist[vertex]:
self.dist[vertex] = cost+self.dist[v]
self.prev[vertex] = v
self.min_list[vertex] = cost+self.dist[v]
self.view_array()
v.self.pick_min_dist()
self.dijkstra(v)
g = ShortestPath()
for start, dest, weight in [(1,2,6),(1,3,2),(1,4,16), (1,7,14), (2,4,5), (2,5,4), (3,2,7), (3,5,3), (3,6,8), (4,7,3), (5,4,4), (5,7,10), (6,7,1)]:
g.create(start, dest, weight)
g.dist[1] = 0
g.prev[1] = None
g.dijkstra(1)
complexity
O(n) to select next destination vertex
O(n) to update d[] and p[] values n times when adjacency matrix is used
selection and update done once for each vertex to which a shortest path is found
total time is O(n^2)
TC can be faster than O(n^2) if the heap is used to select min dist => O(nlogn)
Floyed-Warshall algorithm
all sources all destinations
find shortest path between all vertex pairs
floyd-warshall algorithm
cost matrix
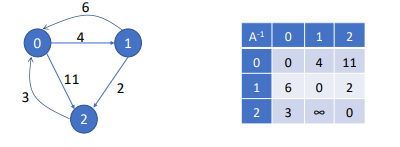
2->1로는 간선이 없다.
비용 행렬을 만들어서 최초에 구한다.
A^k
a^k[i, j] : an element of matrix A^k, is the least cost from i to j via only 0~k vertices, and determined by the smaller value than A^k-1[i, j]
A^k[i,j] = min{A^k-1[i,j], A^k-1[i,k] + A^k-1[k,j]} ( k>= 0 )
given a graph, find cost matrices A0, A1, A2, A3, A4
A^-1
for a cost matrix A-1, an element A-1[i][j] is determined by edge weight between i and j vertices, and if no edge, infinite value is assigned
A^-1[i][j] = cost[i][j]
Floyd-Warshall algorithm
0->0은 구할 필요가 없다.
A0가 끝나고 나면, A1을 만들어낸다.
A1을 경유하니까 행-열을 할 필요가 없다.
스도쿠하는 것 같네
7
6
6
6
5
7
직전 것으로 하는데, 이전 것이 더 짧으면 그걸 가져다 쓴다..
> sudo code
let dist be a |V| * |V| array of minimum distances initialized to infinite
for each vertex v:
dist[v][v] = 0
for each edge (u, v):
dist[u][v] = w(u,v)
Transitive closure Matrix 이행적 폐쇄 행렬
경로가 존재하면 1, 경로가 존재하지 않으면 0으로 표기하는 행렬
A+
Reflective Transitive closure Matrix (반사이행적 폐쇄 행렬)
자기 자신으로 가는 것도 허용한다.
A : adjacency matrix
A+ : transitive closure matrix
A* : Reflexive transitive closure matrix
Acticity Network
정점 작업, 잔선 작업 네트워크
Activity on Vertex, AOV(정점 작업 네트워크)
a directed graph in which the vertices represent tasks or activities and the edges represent precedence relations between tasks
선수관계를 뽑아내고자 하는 것
Topological sort 위상 정렬
DAG Directed Acyclic Graph
possible for a graph with no cycle
algorithm
진입 차수 정점을 queue에 넣는다
정점에 인접한 edge를 제거한다
queue가 empty거나, 모든 vertices에 대하여 방문할 때까지 남은 그래프에 대하여 반복한다
if queue is empty before all nodes are visited, it has a cycle
TC : ?
Topological sort
calculate the in-degrees of all vertices
insert vertices (c1, c2, c4) of 0 in-degree to Q, Q=[c1,c2,c4]
Del c1, 연결된 간선을 제거한다.
c1의 진입 차수가 1로 바뀐다.
스택에서 꺼내서 간선을 계산해준다. 0으로 바꿈
C3가 zero degree vertex
이를 계속 반복한다. c4를 없애고.. .. ..
AOE Network 간선 작업 네트워크
Activity on edge, AOE(간선 작업 네트워크)
is a network for a project that activities are represented on edges(A), and processes are represented on vertices
a process can get started after all inbound activities are complete
AOE network can be applied to search activities affecting to project completion time and analyze the precedence relation between processes
임계 경로 = critical path : the longest path from start process to end process in project
the sum of times of activities in critical path is the project completion time
find a critical pathof the following AOE network
critical path
임계 경로에 놓인 작업을 임계 작업이라고 한다.
E, I
Earliest start time (e) 최단 시작 시간
the earliest time of an activity to start
Latest start time(i)
the latest time of an activity to start without delaying the project
e(7) = 5, e(9) = 13
l(8) = 15
l(6) = 6 : 임계 경로에 있어서 바로 해주어야 한다.
criticallity
임계도
a slack time that an activity affects to the project completion time, and computed by l(i) - e(i)
임계 작업
| activity | earliest time | latest time | 임계도 |
| A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 |
0 0 0 4 6 6 5 9 13 13 22 18 |
9 0 6 13 12 6 11 15 13 13 22 18 |
9 0 6 9 6 0 6 6 0 0 0 0 |
critical path
find all activities that can reduce the project time if they are done quickly
critical activities : A2, A6, A9, A10, A11, A12
activities included in all critical path i common : A2, A6
'Computer Science > 자료구조' 카테고리의 다른 글
| 자료구조 | binary trees, heap sort, threaded binary trees (python 구현) | Trees (0) | 2022.01.08 |
|---|---|
| 자료구조 구현 | selection sort, bubble sort, insertion sort, shell sort, quick sort (python 구현) | 정렬 (0) | 2022.01.08 |
| 자료구조 | Graph | 숙명여대 학점교류 (0) | 2022.01.07 |
| 자료구조 | Graphs | 숙명여대 학점교류 (0) | 2022.01.06 |
| 자료구조 | Binary Search Trees | 숙명여대 학점교류 (0) | 2022.01.06 |