Sort
selection sort
bubble sort
insertion sort
shell sort
quick sort
merge sort
radix sort
sort에 대한 기본적인 설명
정렬이란?
sorting 정렬은 사실 탐색을 하기 위한 '준비'를 하는 단계다.
예를 들면, binary search의 전제 조건은 자료가 정렬되어있어야 한다는 것이었는데, 이것이 단지 binary search 만의 조건이 아니었던 것이다.
sort 문제는 재료가 되는 데이터와 이를 정렬하는 문제로 구성된다.
데이터는 기록한 구조체 형태일 수 있다. 학생 목록을 정렬하는 문제라면, 한 학생 Ri는 학생을 식별하기 위한 key(Ki)와 다른 데이터(성적, 학기, 재학 상태 등)으로 이해할 수 있다.
그리고 이렇게 데이터들이 목록으로 있을 때 정렬 문제란, Ki < Ki+1 (0 <= i <= n-1)의 순서를 만족하는 데이터 목록의 특정한 순열을 찾아내는 것과 같다.
정렬의 종류
정렬에는 internal sort와 external sort가 있다.
internal sort
데이터 규모가 작을 때, 메인 메모리에서 바로 정렬을 실행한다.
external sort
큰 데이터를 여러 개의 부분집합으로 나누고,
각 부분집합을 메인 메모리에서 정렬한 뒤에,
합치는 과정은 외부 저장소에서 하는 정렬의 유형을 말한다.
정렬 성능 평가
data가 움직이는 횟수, key value를 비교하는 횟수 등으로 측정한다
selection sort

<원리>
한 개의 원소만 남을 때까지 정렬된 부분을 재귀적으로 넓힌다
각 재귀 단계에서는 가장 작은 원소, 가장 큰 원소를 왼쪽, 오른쪽 끝으로 보낸다.
<문제>
정렬되지 않은 곳에서 최소/최댓값을 찾아 정렬된 부분으로 보내준다.
시간 복잡도 : O(n^2)
(n : max/min 값을 찾기 위해 순회하는 과정
(n : 위 과정을 재귀적으로 n번 반복
<구현>
스켈레톤 코드
class SelectionSort:
def __init__(self, num):
pass
def __str__(self):
pass
def sort(self):
pass
num = [31,9,10,23,49,15,11,7]
s = SelectionSort()
s.sort()구현 완료 :)
class SelectionSort:
def __init__(self, num):
self.lst = num
self.n = 0
def __str__(self):
for i in self.lst:
print("%2d " % i)
def sort(self):
start = 0
while True:
if start == len(self.lst)-1:
# list에 최종적으로 추가하고
break
tmpMin = self.lst[start]
tmpInd = 0
if start == len(self.lst):
# list에 최종적으로 추가하고
break
for i in range(start, len(self.lst)):
# 최솟값(값, index)을 찾아.
if tmpMin >= self.lst[i]:
tmpMin = self.lst[i]
tmpInd = i
# start 위치와 swap
self.lst[tmpInd] = self.lst[start]
self.lst[start] = tmpMin
start += 1
num = [31,9,10,23,49,15,11,7]
s = SelectionSort(num)
s.sort()
print(s.lst)
bubble sort

<원리>
한 개의 원소만 남을 때까지 정렬된 부분을 재귀적으로 넓힌다
인접한 곳에서 a[i] > a[i+1]이면, swap을 진행한다.
이렇게 해서 가장 큰 key를 리스트의 끝으로 보내는 것이다.
시간 복잡도 : O(n^2)
(n : 순차적으로 swap하면서 리스트 순회
(n : 위 과정을 재귀적으로 n번 반복
<구현>
스켈레톤 코드
class BubbleSort:
def __init__(self, num):
def __str__(self):
def swap(self, a, b):
def sort(self):
num = [31,9,10,23,49,15,11,7]
s = BubbleSort(num)
s.sort()
print(s.lst)구현 완료 :)
class BubbleSort:
def __init__(self, num):
self.lst = num
self.n = 0
def __str__(self):
for i in self.lst:
print("%2d " % i)
def swap(self, a, b):
tmp = self.lst[a]
self.lst[a] = self.lst[b]
self.lst[b] = tmp
def sort(self):
for i in range(len(self.lst)-1):
for j in range(len(self.lst)-1):
if self.lst[j] >= self.lst[j+1]:
self.swap(j, j+1)
num = [31,9,10,23,49,15,11,7]
s = BubbleSort(num)
s.sort()
print(s.lst)
insertion sort
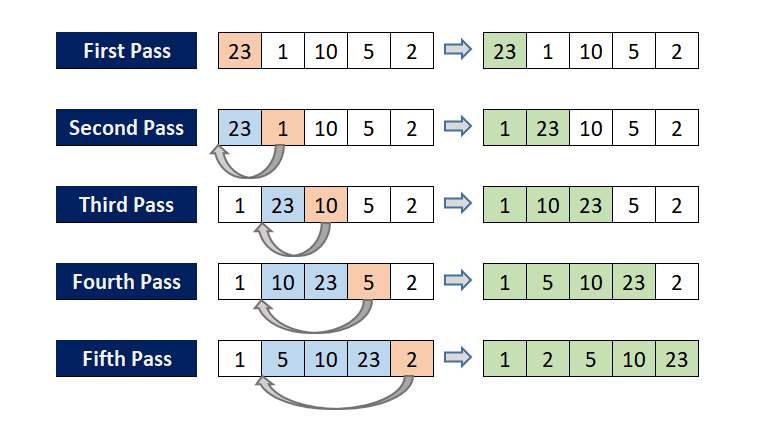
<원리>
한 개의 원소만 남을 때까지 정렬된 부분을 재귀적으로 넓힌다
a[0:n-2]는 이미 정렬된 부분이라고 치고, a[n-1]을 a[0:n-1]에 삽입한다.
시간 복잡도 : O(n^2)
(n : 순차적으로 리스트 순회해서 a[0:n-2] 안 어딘가에 삽입
(n : 위 과정을 재귀적으로 n번 반복
<구현>
스켈레톤 코드
class InsertionSort:
def __init__(self, num):
pass
def __str__(self):
for i in self.lst:
print("%2d " % i)
def sort(self):
pass
num = [31,9,10,23,49,15,11,7]
s = InsertionSort(num)
s.sort()
print(s.lst)구현 완료 :)
class InsertionSort:
def __init__(self, num):
self.lst = num
def __str__(self):
for i in self.lst:
print("%2d " % i)
def sort(self):
for i in range(1, len(self.lst)):
d = 0
tmp = self.lst[i]
for j in range(0, i):
if tmp <= self.lst[j]:
t = self.lst[i]
self.lst[i] = self.lst[j]
self.lst[j] = t
d = 1
else:
continue
num = [31,9,10,23,49,15,11,7]
s = InsertionSort(num)
s.sort()
print(s.lst)
Shell sort
<원리>
Donald Shell이 1959년에 개발한 정렬 알고리즘.
처음으로 quadratic time 장벽을 허물고 linear로 나아간 알고리즘이다.
shell sort는 sub quadratic time algorithm이라고 부른다.
linear와 quadratic 사이에 있다.
shell sort는 삽입 정렬을 활용했으나,
일정 거리를 떨어뜨려서 비교를 해서 효율성을 개선시켰다.
<알고리즘>
shell sort는 gap을 기준으로 부분 리스트를 추출하고,
이 부분 리스트를 삽입 정렬을 이용해서 정렬한다.
gap이 1이 될 때까지 gap을 줄이는 과정을 반복한다.
-> gap은 n/2로 계속해서 나눠주되, floor(n/2)+1로 하는 것이 더 효율적이다.
시간 복잡도 : O(n^3/2)
<구현>
스켈레톤 코드
class shellSort:
def __init__(self, num):
self.lst = num
def __str__(self):
for i in self.lst:
print("%2d " % i)
def sort(self):
pass
num = [31,9,10,23,49,15,11,7]
s = shellSort(num)
s.sort()
print(s.lst)구현 완료 :)
class shellSort:
def __init__(self, num):
self.lst = num
def __str__(self):
for i in self.lst:
print("%2d " % i)
def sort(self):
gap = len(self.lst) // 2
while True:
if gap < 1:
break
for i in range(0, len(self.lst),gap):
tmp = self.lst[i]
for j in range(0, i, gap):
if tmp<= self.lst[j]:
t = self.lst[i]
self.lst[i] = self.lst[j]
self.lst[j] = t
gap //= 2
print(gap)
num = [31,9,10,23,49,15,11,7]
s = shellSort(num)
s.sort()
print(s.lst)
시간 복잡도 분석
faster than : O(n^2)
slower than : O(n)
average : O(n^3/2) -> 'sub-quadratic time'
quick sort 퀵 정렬
<원리>
n <= 1이 될 때까지 재귀적으로 정렬을 진행한다.
각 단계에서는 pivot을 구해, 리스트를 left < pivot < right으로 분리한다.
left, right에 대해 재귀를 반복한다.
pivot을 잘 고르는 게 중요하다. pivot을 고르는 방법에는 크게 세 가지가 있다.
1. 랜덤으로 고르기
2. 0번째 원소 채택
3. Median of Three (0번째 원소, n번째 원소, n/2번째 원소 중 중간값 채택)
<알고리즘>
Median of Three로 pivot을 고른다
pivot을 중심으로 리스트를 left pivot right으로 분리한다.
-> 분리하는 알고리즘 : in-place partition

i < j인 동안 다음을 반복한다.
왼쪽 포인터인 i는 키우고 오른쪽 포인터인 j는 줄인다.
만약 list[왼쪽] > pivot이면, 잠시 멈춤
만약 list[오른쪽] < pivot이면, 잠시 멈춤
swap(왼쪽, 오른쪽)
i == j가 되면, swap(pivot, list[j])를 해준다.
left, right에 대해 재귀호출 실행
시간 복잡도
average time complexity : O(n*logn)
worst case time complexity : O(n^2)
<구현>
스켈레톤 코드
num = [31,9,10,23,49,15,11,7]
s = shellSort(num)
s.sort()
print(s.lst)
class QuickSort:
def __init__(self, num):
pass
def swap(self, a, b):
pass
def sort(self, left, right):
pass
num = [31,9,10,23,49,15,11,7]
s = QuickSort(num)
s.sort()
print(s.lst)구현 완료 :)
class QuickSort:
def __init__(self, num):
self.lst = num
def MedianofThree(self, left, right):
mid = self.lst[(left+right)//2]
lft = self.lst[left]
rt = self.lst[right]
if (mid <= rt <= lft) or (lft <= rt <= mid):
return right
elif (rt < mid < lft) or (lft < mid < rt):
return (left+right)//2
else:
return left
def sort(self, left, right):
# 재귀적인 반복
if left >= right:
print("HI")
return self.lst
pivot = self.MedianofThree(left, right)
lft = left
rt = right
# partitining
while True:
if lft >= rt:
self.lst[pivot], self.lst[lft] = self.lst[lft] , self.lst[pivot]
break
if self.lst[lft] <= pivot:
lft += 1
if self.lst[rt] >= pivot:
rt -= 1
if self.lst[lft] > pivot and self.lst[rt] < pivot:
self.lst[lft], self.lst[rt] = self.lst[rt] , self.lst[lft]
self.sort(left, pivot-1)
self.sort(pivot+1, right)
num = [31,7,6]
s = QuickSort(num)
s.sort(0, len(num)-1)
print(s.lst)
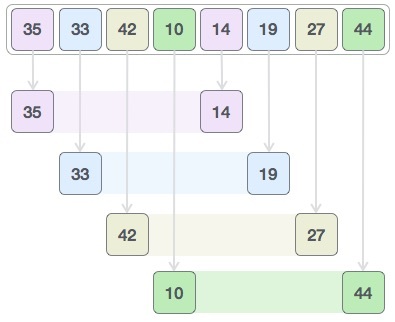
merge sort
<원리>
divide and conquer
divide : 각 요소를 계속해서 쪼갠다.
merge : 각 segment를 정렬하면서 합친다.
<알고리즘>
- 분할 Divide : 입력 배열을 2개의 부분 배열로 분할한다
- 정복 Conquer : 부분 배열을 정렬한다
리스트의 값을 하나씩 비교해서 두 개의 리스트 중 작은 값을 새로운 리스트에 옮긴다.
만약 하나의 리스트가 끝나면, 나머지 리스트의 값을 새로운 리스트에 복사한다.
새로운 리스트를 원래의 리스트로 옮긴다.
- 결합 Combine : 부분 배열을 하나의 배열에 합병한다
시간 복잡도
downward passing : O(n)
upward passing : O(nlogn)
Total = O(nlogn)
<구현>
스켈레톤 코드
class MergeSort:
def __init__(self, num):
self.lst = num
def swap(self, a, b):
pass
def mergesort(self, left, right):
pass
def merge(self, left, mid, right):
pass
num = [31,7,6]
s = MergeSort(num)
s.sort(0, len(num)-1)
print(s.lst)구현 완료 :)
class MergeSort:
def __init__(self, num):
self.lst = num
def swap(self, a, b):
self.lst[a], self.lst[b] = self.lst[b], self.lst[a]
def mergesort(self, left, right):
# 종료 조건
if left < right: # 0 1
# 원소가 1개가 될 때까지 분리를 반복한다.
mid = ((left + right) // 2)
self.mergesort(left, mid) # 0 0
self.mergesort(mid+1, right) # 1 1
self.merge(left, mid, right) # 0 1 1
def merge(self, left, mid, right):
# left, mid, right 영역에 대해서 sort하면서 merge하기
tmp = []
lptr = left
rptr = mid +1
while lptr <= mid and rptr <= right:
if self.lst[lptr] < self.lst[rptr]:
tmp.append(self.lst[lptr])
lptr += 1
elif self.lst[lptr] >= self.lst[rptr]:
tmp.append(self.lst[rptr])
rptr += 1
while lptr <= mid:
tmp.append(self.lst[lptr])
lptr += 1
while rptr <= right:
tmp.append(self.lst[rptr])
rptr += 1
index = left
for i in tmp:
self.lst[index] = i
index += 1
print("merge sort")
num = [31,7,6,3,4,5,1]
s = MergeSort(num)
s.mergesort(0, len(num)-1)
print(s.lst)radix sort 기수 정렬
<원리>
3 가지 스텝을 반복하는 정렬 방법이다.
element 간에 비교 연산을 하지 않고 계산해서 정렬 속도가 빠르다.
그러나, 기수 테이블만큼의 메모리가 더 필요하다.
step 0. comparison : LSD least-significant digit부터 MSD most significant digit까지 비교한다.
가장 낮은 자리수(LSD)부터 큐 버킷에 차례로 데이터를 둔다.
그 다음에는 다시 버킷에서 데이터를 가져와서 자리수를 높여가면서 MSD까지 반복한다.
step 1. distribution
step 2. merge
큐 버킷에서 차례로 데이터를 꺼내오면, 정렬이 완료된다.
시간 복잡도
O(k*n)으로 알려져있다. (k는 자리수)
위치 표기(positional notation)을 통해서 비교하지 않고 정렬하는
non-comparative integer sorting algorithm 알고리즘의 형태이다.
<구현>
스켈레톤 코드
class Queue:
pass
class RadixSort:
def __init__(self, num):
self.lst = num
def radixsort(self, degree):
pass
# 0부터 9까지 Bucket을 준비한다. (Queue)
# 데이터를 보며 가장 낮은 차수에 대해 Bucket에 데이터를 넣는다.
# 차례로 데이터를 도로 가져온다.
# 다시 이 리스트를 그대로 자리수를 높여 Bucket에 데이터를 넣는다.
print("radix sort")
num = [31,7,6,3,4,5,1]
s = RadixSort(num)
s.radixsort(0)
print(s.lst)구현 완료 :)
import math
class Queue:
# FIFO
def __init__(self):
# 0부터 9까지 queue를 준비함
self.line0 = []
self.line1 = []
self.line2 = []
self.line3 = []
self.line4 = []
self.line5 = []
self.line6 = []
self.line7 = []
self.line8 = []
self.line9 = []
self.full = [self.line0, self.line1, self.line2,self.line3,self.line4,self.line5,self.line6,self.line7,self.line8,self.line9]
def enqueue(self, num, degree):
# num == 1, degree == 1이면,
# return num % (pow(10, degree))
print(pow(10, degree))
i = (num % pow(10, degree+1))//pow(10, degree) # 1, 1 => 1, 2, 1 =? 2
self.full[i].append(num)
def dequeueAll(self):
tmp = []
for i in [self.line0, self.line1, self.line2,self.line3,self.line4,self.line5,self.line6,self.line7,self.line8,self.line9]:
while len(i) > 0:
tmp.append(i.pop(0))
return tmp
class RadixSort:
def __init__(self, num, maxdegree):
self.lst = num
self.max = maxdegree
def radixsort(self, degree):
# 종료 조건
if degree > self.max:
return
# 0부터 9까지 Bucket을 준비한다. (Queue)
tmp = Queue()
# 데이터를 보며 가장 낮은 차수에 대해 Bucket에 데이터를 넣는다.
for i in self.lst:
tmp.enqueue(i, degree)
# 차례로 데이터를 도로 가져온다.
self.lst = tmp.dequeueAll()
# 다시 이 리스트를 그대로 자리수를 높여 Bucket에 데이터를 넣는다.
self.radixsort(degree+1)
print("radix sort")
num = [31,7,6,3,4,5,1]
maxdegree = 1
s = RadixSort(num, maxdegree)
s.radixsort(0)
print(s.lst)
'Computer Science > 자료구조' 카테고리의 다른 글
| 자료구조 | Binary Search Trees, AVL tree, B-Trees | python 구현 (0) | 2022.01.08 |
|---|---|
| 자료구조 | binary trees, heap sort, threaded binary trees (python 구현) | Trees (0) | 2022.01.08 |
| 자료구조 | Shortest Path and Activity Network | 숙명여대 학점교류 (0) | 2022.01.07 |
| 자료구조 | Graph | 숙명여대 학점교류 (0) | 2022.01.07 |
| 자료구조 | Graphs | 숙명여대 학점교류 (0) | 2022.01.06 |